
ЁОЬтФПЁПШчЭМ(1),дкЁїABCжа,AB=BC,PЮЊABБпЩЯвЛЕу,СЌНгCP,вдPAЁЂPCЮЊСкБпзї![]() APCDЃЌACгыPDЯрНЛгкЕуEЃЌвбжЊЁЯABC=ЁЯAEP=
APCDЃЌACгыPDЯрНЛгкЕуEЃЌвбжЊЁЯABC=ЁЯAEP=![]() (0Ёу<
(0Ёу<![]() <90Ёу).
<90Ёу).
(1)ЧѓжЄ: ЁЯEAP=ЁЯEPA;
(2)![]() APCDЪЧЗёЮЊОиаЮ?ЧыЫЕУїРэгЩ;
APCDЪЧЗёЮЊОиаЮ?ЧыЫЕУїРэгЩ;
(3)ШчЭМ(2),FЮЊBCжаЕу,СЌНгFP,НЋЁЯAEPШЦЕуEЫГЪБеыа§зЊЪЪЕБЕФНЧЖШ,ЕУЕНЁЯMEN(ЕуMЁЂNЗжБ№ЪЧЁЯMENЕФСНБпгыBAЁЂFPбгГЄЯпЕФНЛЕу).ВТЯыЯпЖЮEMгыENжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТл.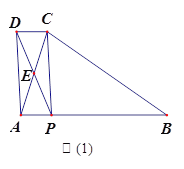
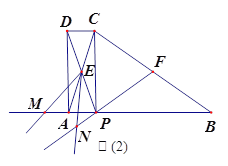
ЁОД№АИЁП(1)МћНтЮіЃЛ
(2)![]() APCDЪЧОиаЮ.ЃЌРэгЩМћНтЮіЃЛ
APCDЪЧОиаЮ.ЃЌРэгЩМћНтЮіЃЛ
(3)EM=ENЃЌРэгЩМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнAB=BCПЩжЄЁЯCAB=ЁЯACBЃЌдђдкЁїABCгыЁїAEPжаЃЌгаСНИіНЧЖдгІЯрЕШЃЌИљОнШ§НЧаЮФкНЧКЭЖЈРэЃЌМДПЩжЄЕУЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉжЊЁЯEPA=ЁЯEAPЃЌдђAC=DPЃЌИљОнЖдНЧЯпЯрЕШЕФЦНааЫФБпаЮЪЧОиаЮМДПЩЧѓжЄЃЛ
ЃЈ3ЃЉПЩвджЄУїЁїEAMЁеЁїEPNЃЌДгЖјЕУЕНEM=ENЃЎ
жЄУїЃК(1)дкЁїABCКЭЁїAEPжа,
![]() ЁЯABC=ЁЯAEP,ЁЯBAC=ЁЯEAP,
ЁЯABC=ЁЯAEP,ЁЯBAC=ЁЯEAP,
![]() ЁЯACB=ЁЯAPE,
ЁЯACB=ЁЯAPE,
дкЁїABCжа,AB=BC.![]() ЁЯACB=ЁЯBAC,
ЁЯACB=ЁЯBAC,
![]() ЁЯEPA=ЁЯEAP,
ЁЯEPA=ЁЯEAP,
(2)![]() APCDЪЧОиаЮ.
APCDЪЧОиаЮ.
![]() ЫФБпаЮAPCDЪЧЦНааЫФБпаЮ,
ЫФБпаЮAPCDЪЧЦНааЫФБпаЮ,
![]() AC=2EA,PD=2EP.
AC=2EA,PD=2EP.
гЩ(1)жЊ, ЁЯEPA=ЁЯEAP.
![]() EA=EPЃЌНјЖјAC=PD
EA=EPЃЌНјЖјAC=PD
![]()
![]() APCDЪЧОиаЮ.
APCDЪЧОиаЮ.
(3)EM=EN
![]() EA=EP,
EA=EP,![]() ЁЯEPA=90Ёу -
ЁЯEPA=90Ёу -![]()
![]() ЁЯEAM=180Ёу-ЁЯEAP =180Ёу-ЁЯEPA= 180Ёу-(90Ёу-
ЁЯEAM=180Ёу-ЁЯEAP =180Ёу-ЁЯEPA= 180Ёу-(90Ёу-![]() )=90Ёу+
)=90Ёу+![]()
гЩ(2)жЊ, ЁЯCPB=90Ёу,FЪЧBCЕФжаЕу,![]() FP=FB,
FP=FB,
![]() ЁЯFPB=ЁЯABC=
ЁЯFPB=ЁЯABC=![]() ЃЌ
ЃЌ
![]() ЁЯEPN=ЁЯEPA+ЁЯAPN=ЁЯEPA+ЁЯFPB=90Ёу -
ЁЯEPN=ЁЯEPA+ЁЯAPN=ЁЯEPA+ЁЯFPB=90Ёу -![]() +
+![]() =90Ёу+
=90Ёу+![]()
![]() ЁЯEAM=ЁЯEPN
ЁЯEAM=ЁЯEPN
![]() ЁЯAEPШЦЕуEЫГЪБеыа§зЊЪЪЕБЕФНЧЖШЃЌЕУЕНЁЯMENЃЌ
ЁЯAEPШЦЕуEЫГЪБеыа§зЊЪЪЕБЕФНЧЖШЃЌЕУЕНЁЯMENЃЌ
![]() ЁЯAEP-ЁЯAEN =ЁЯMEN-ЁЯAEN,МДЁЯMEA=ЁЯNEP.
ЁЯAEP-ЁЯAEN =ЁЯMEN-ЁЯAEN,МДЁЯMEA=ЁЯNEP.
![]() ЁїEAMЁеЁїEPN,
ЁїEAMЁеЁїEPN,
![]() EM=EN.
EM=EN.


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
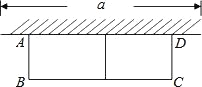
ЁОЬтФПЁПШчЭМЃЌгаГЄЮЊ 24m ЕФРщАЪЃЌЯжвЛУцРћгУЧНЃЈЧНЕФзюДѓПЩгУГЄЖШ a ЮЊ 10mЃЉЮЇГЩжаМфИєгавЛЕРРщАЪЕФГЄЗНаЮЛЈЦдЃЌЩшЛЈЦдЕФПэ AB ЮЊ xmЃЌУцЛ§ЮЊ Sm2ЃЎ
ЃЈ1ЃЉ Чѓ S гы x ЕФКЏЪ§ЙиЯЕЪНМА x жЕЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉ вЊЮЇГЩУцЛ§ЮЊ 45m2 ЕФЛЈЦдЃЌAB ЕФГЄЪЧЖрЩйУзЃП
ЃЈ3ЃЉ ЕБ AB ЕФГЄЪЧЖрЩйУзЪБЃЌЮЇГЩЕФЛЈЦдЕФУцЛ§зюДѓЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигк x ЕФКЏЪ§ y=ЃЈmЉ1ЃЉx2+2x+m ЭМЯѓгызјБъжсжЛга 2 ИіНЛЕуЃЌдђm=_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§y=kx+bгыЗДБШР§КЏЪ§y=![]() ЃЈmЁй0ЃЉЕФЭМЯѓНЛгкЕуAЃЈ3ЃЌ1ЃЉЃЌЧвЙ§ЕуBЃЈ0ЃЌЉ2ЃЉЃЎ
ЃЈmЁй0ЃЉЕФЭМЯѓНЛгкЕуAЃЈ3ЃЌ1ЃЉЃЌЧвЙ§ЕуBЃЈ0ЃЌЉ2ЃЉЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЙћЕуPЪЧxжсЩЯвЛЕуЃЌЧвЁїABPЕФУцЛ§ЪЧ3ЃЌЧѓЕуPЕФзјБъЃЎ
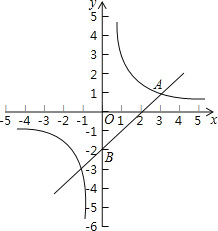
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
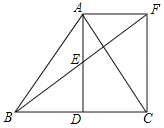
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌDЪЧBCБпЩЯвЛЕуЃЌEЪЧADЕФжаЕуЃЌЙ§ЕуAзїBCЕФЦНааЯпНЛBEЕФбгГЄЯпгкFЃЌЧвAF=CDЃЌСЌНгCFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAEFЁеЁїDEBЃЛ
ЃЈ2ЃЉШєAB=ACЃЌЪдХаЖЯЫФБпаЮADCFЕФаЮзДЃЌВЂжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНШЫЯрдМжмФЉЕЧЛЈЙћЩНЃЌМзЁЂввСНШЫОрЕиУцЕФИпЖШ![]() ЃЈУзЃЉгыЕЧЩНЪБМф
ЃЈУзЃЉгыЕЧЩНЪБМф![]() ЃЈЗжЃЉжЎМфЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЌИљОнЭМЯѓЫљЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈЗжЃЉжЎМфЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЌИљОнЭМЯѓЫљЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉМзЕЧЩНЩЯЩ§ЕФЫйЖШЪЧУПЗжжг УзЃЌввдк![]() ЕиЪБОрЕиУцЕФИпЖШ
ЕиЪБОрЕиУцЕФИпЖШ![]() ЮЊ УзЃЛ
ЮЊ УзЃЛ
ЃЈ2ЃЉШєввЬсЫйКѓЃЌввЕФЕЧЩНЩЯЩ§ЫйЖШЪЧМзЕЧЩНЩЯЩ§ЫйЖШЕФ3БЖЃЌЧыЧѓГіввЕЧЩНШЋГЬжаЃЌОрЕиУцЕФИпЖШ![]() ЃЈУзЃЉгыЕЧЩНЪБМф
ЃЈУзЃЉгыЕЧЩНЪБМф![]() ЃЈЗжЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈЗжЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ3ЃЉЕЧЩНЖрГЄЪБМфЪБЃЌМзЁЂввСНШЫОрЕиУцЕФИпЖШВюЮЊ50УзЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌBDЦНЗжЁЯABCЃЌЧвADЁЭBDЃЌEЮЊACЕФжаЕуЃЌADЃН6cmЃЌBDЃН8cmЃЌBCЃН16cmЃЌдђDEЕФГЄЮЊ_____cmЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁбO ЕФжБОЖЮЊ 4ЃЌAB ЪЧЁбO ЕФЯвЃЌЁЯAOB=120ЁуЃЌЕу P дкЁбO ЩЯЃЌШєЕу PЕНжБЯп AB ЕФОрРыЮЊ 1ЃЌдђЁЯPAB ЕФЖШЪ§ЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдке§ЗНаЮABCDжаЃЌЖдНЧЯпBDЫљдкЕФжБЯпЩЯгаСНЕуEЁЂFТњзуBE=DFЃЌСЌНгAEЁЂAFЁЂCEЁЂCFЃЌШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABEЁеЁїADFЃЛ
ЃЈ2ЃЉЪдХаЖЯЫФБпаЮAECFЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com