
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
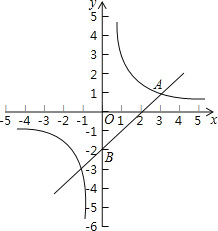
【答案】(1)y=![]() ;y=x-2;(2)(0,0)或(4,0)
;y=x-2;(2)(0,0)或(4,0)
【解析】试题分析:(1)利用待定系数法即可求得函数的解析式;
(2)首先求得AB与x轴的交点,设交点是C,然后根据S△ABP=S△ACP+S△BCP即可列方程求得P的横坐标.
试题解析:(1)∵反比例函数y=![]() (m≠0)的图象过点A(3,1),
(m≠0)的图象过点A(3,1),
∴3=![]()
∴m=3.
∴反比例函数的表达式为y=![]() .
.
∵一次函数y=kx+b的图象过点A(3,1)和B(0,-2).
∴![]() ,
,
解得: ![]() ,
,
∴一次函数的表达式为y=x-2;
(2)令y=0,∴x-2=0,x=2,
∴一次函数y=x-2的图象与x轴的交点C的坐标为(2,0).
∵S△ABP=3,
![]() PC×1+
PC×1+![]() PC×2=3.
PC×2=3.
∴PC=2,
∴点P的坐标为(0,0)、(4,0).


科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 与
与![]() (k≠0)的图象相交于点P(1,-6).
(k≠0)的图象相交于点P(1,-6).
(1)求一次函数![]() 的解析式;
的解析式;
(2)若点Q(m,n)在函数![]() 的图象上,求2n-6m+9的值.
的图象上,求2n-6m+9的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌AB,放置在教学楼的顶部(如图所示)。小明在操场上的点D处,用1m高的测角仪CD,从点C测得宣传牌的底部B的仰角为37,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌顶部A仰角为45.已知教学楼高BM=17米,且点A、B、M在同一直线上,求宣传牌AB高度(结果精确到0.1米。参考数据:![]() ,sin37≈0.60,cos37≈0.81,tan37≈0.75).
,sin37≈0.60,cos37≈0.81,tan37≈0.75).

查看答案和解析>>
科目:初中数学 来源: 题型:
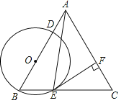
【题目】如图,在等边![]() 中,点
中,点![]() 在边
在边![]() 上,
上,![]() 过点
过点![]() 且分别与边
且分别与边![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() 、
、![]() 是
是![]() 上的点,判断下列说法错误的是( )
上的点,判断下列说法错误的是( )
A. 若![]() ,则
,则![]() 是
是![]() 的切线 B. 若
的切线 B. 若![]() 是
是![]() 的切线,则
的切线,则![]()
C. 若![]() ,则
,则![]() 是
是![]() 的切线 D. 若
的切线 D. 若![]() ,则
,则![]() 是
是![]() 的切线
的切线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
例如:某三角形三边长分别是2,4,![]() ,因为
,因为![]() ,所以这个三角形是奇异三角形.
,所以这个三角形是奇异三角形.
(1)根据定义:“等边三角形是奇异三角形”这个命题是______命题(填“真”或“假命题”);
(2)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,若
,若![]() 是奇异三角形,求
是奇异三角形,求![]() ;
;
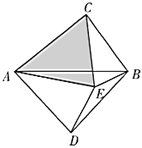
(3)如图,以![]() 为斜边分别在
为斜边分别在![]() 的两侧作直角三角形,且
的两侧作直角三角形,且![]() ,若四边形
,若四边形![]() 内存在点
内存在点![]() ,使得
,使得![]() ,
,![]() .
.
①求证:![]() 是奇异三角形;
是奇异三角形;
②当![]() 是直角三角形时,求
是直角三角形时,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC和△ADE中,∠BAC=∠EAD,AB=AC,AD=AE,连接CD、AE交于点F.
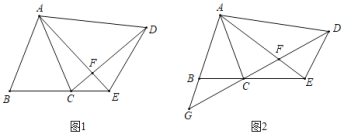
(1)求证:BE=CD.
(2)当∠BAC=∠EAD=30°,AD⊥AB时(如图2),延长DC、AB交于点G,请直接写出图中除△ABC、△ADE以外的等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
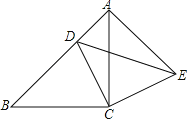
【题目】如图,△ABC是等腰直角三角形,且∠ACB=90°,点D是AB边上的一点(点D不与A,B重合),连接CD,过点C作CE⊥CD,且CE=CD,连接DE,AE.
(1)求证:△CBD≌△CAE;
(2)若AD=4,BD=8,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com