
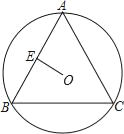
【题目】已知:⊙O为△ABC的外接圆,AB=AC,E是AB的中点,连OE,OE=![]() ,BC=8,则⊙O的半径为( )
,BC=8,则⊙O的半径为( )
A. 3 B. ![]() C.
C. ![]() D. 5
D. 5
 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
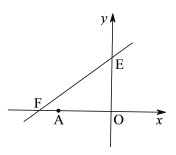
【题目】如图,直线![]() 与x轴、y轴分别相交于点F,E,点A的坐标为(-6,0),P(x,y)是直线
与x轴、y轴分别相交于点F,E,点A的坐标为(-6,0),P(x,y)是直线![]() 上的一个动点.
上的一个动点.
(1)试写出点P在运动过程中,△OAP的面积S与x的函数关系式;
(2)当点P运动到什么位置,△OAP的面积为![]() ,求出此时点P的坐标.
,求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
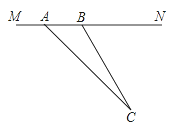
【题目】目前,崇明县正在积极创建全国县级文明城市,交通部门一再提醒司机:为了安全,请勿超速,并在进一步完善各类监测系统,如图,在陈海公路某直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
(参考数据:![]() =1.41,
=1.41,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:如图1所示的图形,像我们常见的学习用品—圆规.我们不妨把这样图形叫做“规形图”.
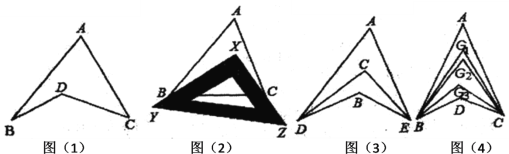
(1)观察“规形图”,试探究![]() 与
与![]() 、
、![]() 、
、![]() 之间的关系,并说明理由;
之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺![]() 放置在
放置在![]() 上,使三角尺的两条直角边
上,使三角尺的两条直角边![]() 、
、![]() 恰好经过点
恰好经过点![]() 、
、![]() ,
,![]() ,则
,则![]() ________________;
________________;
②如图3,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
③如图4,![]() ,
,![]() 的
的![]() 等分线相交于点
等分线相交于点![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
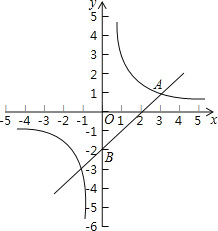
查看答案和解析>>
科目:初中数学 来源: 题型:
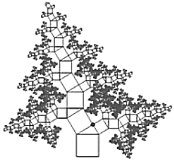
【题目】勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.如图所示,是一棵由正方形和含![]() 角的直角三角形按一定规律长成的勾股树,树的主干自下而上第一个正方形和第一个直角三角形的面积之和为
角的直角三角形按一定规律长成的勾股树,树的主干自下而上第一个正方形和第一个直角三角形的面积之和为![]() ,第二个正方形和第二个直角三角形的面积之和为
,第二个正方形和第二个直角三角形的面积之和为![]() ,…,第
,…,第![]() 个正方形和第
个正方形和第![]() 个直角三角形的面积之和为
个直角三角形的面积之和为![]() .
.
设第一个正方形的边长为1.
请解答下列问题:
(1)![]() ______.
______.
(2)通过探究,用含![]() 的代数式表示
的代数式表示![]() ,则
,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.

(1)求抛物线的解析式;
(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;
(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com