
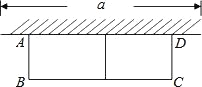
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?
【答案】(1)S=﹣3x2+24x,![]() ≤x< 8;(2) 5m;(3)46.67m2
≤x< 8;(2) 5m;(3)46.67m2
【解析】
(1)根据AB为xm,BC就为(24-3x),利用长方体的面积公式,可求出关系式;
(2)将S=45代入(1)中关系式,可求出x即AB的长;
(3)当墙的宽度为最大时,有最大面积的花圃.此故可求.
(1)根据题意,得S=x(24﹣3x),
即所求的函数解析式为:S=﹣3x2+24x,
又∵0<24﹣3x≤10,
∴![]() ≤x< 8;
≤x< 8;
(2)根据题意,设AB长为x,则BC长为24﹣3x,
∴﹣3x2+24x=45,
整理,得x2﹣8x+15=0,
解得x=3或5,
当x=3时,BC=24﹣9=15>10不成立,
当x=5时,BC=24﹣15=9<10成立,
∴AB长为5m;
(3)S=24x﹣3x2=﹣3(x﹣4)2+48,
∵墙的最大可用长度为10m,0≤BC=24﹣3x≤10,
∴![]() ≤x< 8,
≤x< 8,
∵对称轴x=4,开口向下,
∴当x=![]() m,有最大面积的花圃,
m,有最大面积的花圃,
即:x=![]() m,
m,
最大面积为:=24×![]() ﹣3×(
﹣3×(![]() )2=46.67m2
)2=46.67m2


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在直角坐标系中,O为坐标原点,A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程x2﹣4x=12;
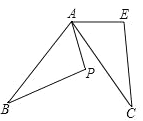
(2)如图,△ABP是由△ACE绕A点旋转得到的,若∠APB=110°,∠B=30°,∠PAC=20°,求旋转角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各减去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为( )

A. 10×6﹣4×6x=32 B. (10﹣2x)(6﹣2x)=32
C. (10﹣x)(6﹣x)=32 D. 10×6﹣4x2=32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F
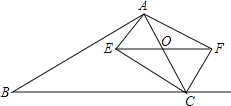
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形CEAF是矩形?请证明你的结论.
(3)在第(2)问的结论下,若AE=3,EC=4,AB=12,BC=13,请直接写出凹四边形ABCE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
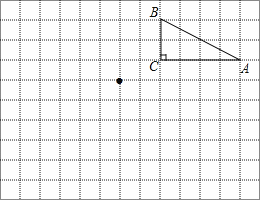
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,点A,B,C都是格点.
(1)将△ABC向左平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2,请画出△A2B2C2;
(3)作出△ABC关于直线l对称的△A3B3C3,使A,B,C的对称点分别是A3,B3,C3;
(4)△A2B2C2与△A3B3C3成_____________,△A1B1C1与△A2B2C2成_____________(填“中心对称”或“轴对称”).如果成中心对称请你在图中确定其对称中心点P的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O是△ABC的外接圆,连接AO,若∠BAC+∠OAB=90°.
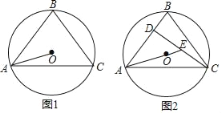
(1)求证:![]()
(2)如图2,作CD⊥AB交于D,AO的延长线交CD于E,若AO=3,AE=4,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
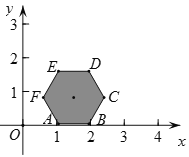
【题目】如图,在平面直角坐标xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,每旋转60°为滚动1次,那么当正六边形ABCDEF滚动2017次时,点F的坐标是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作![]() APCD,AC与PD相交于点E,已知∠ABC=∠AEP=
APCD,AC与PD相交于点E,已知∠ABC=∠AEP=![]() (0°<
(0°<![]() <90°).
<90°).
(1)求证: ∠EAP=∠EPA;
(2)![]() APCD是否为矩形?请说明理由;
APCD是否为矩形?请说明理由;
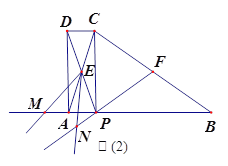
(3)如图(2),F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.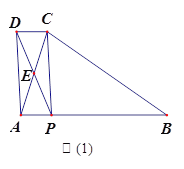
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com