
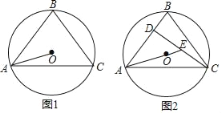
【题目】如图1,⊙O是△ABC的外接圆,连接AO,若∠BAC+∠OAB=90°.
(1)求证:![]()
(2)如图2,作CD⊥AB交于D,AO的延长线交CD于E,若AO=3,AE=4,求线段AC的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)连BO并延长BO交AC于T.只要证明BT⊥AC,利用垂径定理即可解决问题;
(2)延长AO并交⊙O于F,连接CF.在Rt△AFC中,求出CF,AF即可解决问题.
(1)证明:连BO并延长BO交AC于T.
∵ AO=BO,
∴∠ OAB=∠ OBA,
又∵ ∠ BAC+∠ OAB=90°,
∴ ∠ BAC+∠ OBA=90°,
∴ ∠ BTA=90°,
∴ BT⊥AC,
∴ ![]() .
.
(2)延长AO并交![]() O 于F,连接CF.
O 于F,连接CF.
∵ CD⊥ AB于D,
∴ ∠ CDA=90°,
∴ ∠ OAB+∠ A ED=90°,
∵ ∠ OAB+∠ BAC=90°,
∴ ∠ AED=∠ BAC=∠ FEC,
∵ AF为⊙ O直径,
∴ ∠ ACF=90°,
同理:∠ FCE=∠ BAC,
∴ ∠ FEC= ∠ FCE,
∴FE=FC,
∵AO=3,AE=4,
∴OE=1,FE=FC=2,
在Rt△FCA中
∴ AC=![]() =4
=4![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】“天生雾、雾生露、露生耳”,银耳是一种名贵食材,富含人体所需的多种氨基酸和微量元素,具有极高的药用价值和食用价值.某银耳培育基地的银耳成熟了,需要采摘和烘焙.现准备承包给甲和乙两支专业采摘队,若承包给甲队,预计12天才能完成,为了减小银耳因气候变化等原因带来的损失,现决定由甲、乙两队同时采摘,则可以提前8天完成任务.
(1)若单独由乙队采摘,需要几天才能完成?
(2)若本次一共采摘了300吨新鲜银耳,急需在9天内进行烘焙技术处理.已知甲、乙两队每日烘焙量相当,甲队单独加工(烘焙)![]() 天完成100吨后另有任务,剩下的200吨由乙队加工(烘焙),乙队刚好在规定的时间内完工.若甲、乙两队从采摘到加工,每日工资分别是600元和1000元.问:银耳培育基地此次需要支付给采摘队的总工资是多少?
天完成100吨后另有任务,剩下的200吨由乙队加工(烘焙),乙队刚好在规定的时间内完工.若甲、乙两队从采摘到加工,每日工资分别是600元和1000元.问:银耳培育基地此次需要支付给采摘队的总工资是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
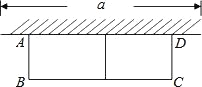
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
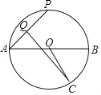
【题目】如图,AB为⊙O的直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为( )
A. 3 B. 1+![]() C. 1+3
C. 1+3![]() D. 1+
D. 1+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+(2t﹣2)x+t2﹣2t﹣3与x轴交于A、B两点(A在B左侧),与y轴交于点C.
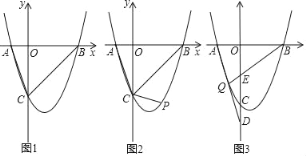
(1)如图1,当t=0时,连接AC、BC,求△ABC的面积;
(2)如图2,在(1)的条件下,若点P为在第四象限的抛物线上的一点,且∠PCB+∠CAB=135°,求P点坐标;
(3)如图3,当﹣1<t<3时,若Q是抛物线上A、C之间的一点(不与A、C重合),直线QA、QB分别交y轴于D、E两点.在Q点运动过程中,是否存在固定的t值,使得CE=2CD.若存在,求出t值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com