
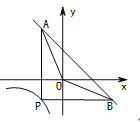
【题目】如图,P为反比例函数![]() (x<0)在第三象限内图象上的一点,过点P分别作x轴、y轴的垂线交一次函数y=-x+4的图像于点A、B.若AO、BO分别平分∠BAP,∠ABP ,则k的值为___________.
(x<0)在第三象限内图象上的一点,过点P分别作x轴、y轴的垂线交一次函数y=-x+4的图像于点A、B.若AO、BO分别平分∠BAP,∠ABP ,则k的值为___________.
【答案】8
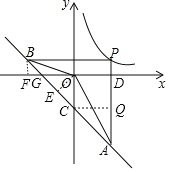
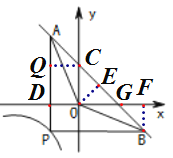
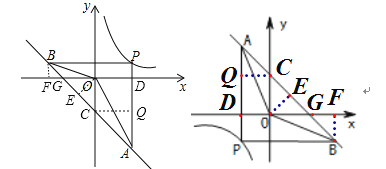
【解析】分析: 作BF⊥x轴,OE⊥AB,CQ⊥AP,易证△BOE∽△AOD,根据相似三角形对应边比例相等的性质即可求出k的值.
详解: 作BF⊥x轴,OE⊥AB,CQ⊥AP;设P点坐标(n,![]() ),
),
∵直线AB函数式为y=-x+4,PB⊥y轴,PA⊥x轴,
∴∠PBA=∠PAB=45°,
∴PA=PB,
∵P点坐标(-n,-![]() ),
),
∴OD=CQ=n,
∴AD=AQ+DQ=n+4;
∵当x=0时,y=-x+4=4,
∴OC=DQ=4,GE=OE=![]() OC=2
OC=2![]() ;
;
同理可证:BG=![]() BF=
BF=![]() PD=
PD=![]() ,
,
∴BE=BG+EG=![]() +2
+2![]() ;
;
∵∠APB=90°,
∴∠PAB+∠PBA=90°.
∵AO、BO分别平分∠BAP,∠ABP ,
∴∠OBE+∠OAE=45°,
∵∠DAO+∠OAE=45°,
∴∠DAO=∠OBE,
在△BOE和△AOD中,
∵∠DAO=∠OBE,
∠BEO=∠ADO=90°,
∴△BOE∽△AOD;
∴![]() ,
,
∴![]() ;
;
整理得:nk+2n2=8n+2n2,
化简得:k=8;
故答案为:8.


科目:初中数学 来源: 题型:
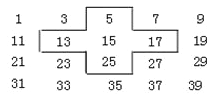
【题目】将连续的奇数1,3,5,7,9…排成如下的数表:
(1)十字框中的五个数的平均数与15有什么关系?
(2)若将十字框上下左右平移,可框住另外的五个数,这五个数的和能等于315吗?若能,请求出这五个数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC为矩形,点B坐标为(4,2),A,C分别在x轴,y轴上,点F在第一象限内,OF的长度不变,且反比例函数![]() 经过点F.
经过点F.
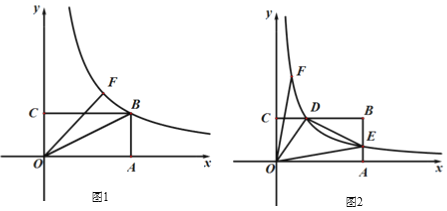
(1)如图1,当F在直线y = x上时,函数图象过点B,求线段OF的长.
(2)如图2,若OF从(1)中位置绕点O逆时针旋转,反比例函数图象与BC,AB相交,交点分别为D,E,连结OD,DE,OE.
①求证:CD=2AE.
②若AE+CD=DE,求k.
③设点F的坐标为(a,b),当△ODE为等腰三角形时,求(a+b)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线y=x+1与抛物线y=2x2相交于A、B两点,与y轴交于点M,M、N关于x轴对称,连接AN、BN.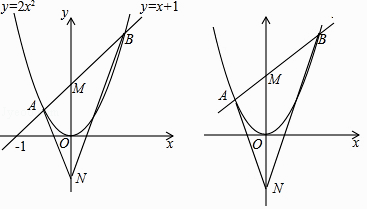
(1)①求A、B的坐标;②求证:∠ANM=∠BNM;
(2)如图2,将题中直线y=x+1变为y=kx+b(b>0),抛物线y=2x2变为y=ax2(a>0),其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结 合.研究数轴我们发现了许多重要的规律:若数轴上点 A、点 B 表示的数分别为 a、b,则A、B 两点之间的距离 AB= ![]() ,线段 AB 的中点表示的数为
,线段 AB 的中点表示的数为![]() .
.
【问题情境】如图,数轴上点A表示的数为-2,点B表示的数为8,点P从点 A 出发, 以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒 2个单 位长度的速度向左匀速运动,设运动时间为t秒(t>0).
【综合运用】(1) 填空:
①A、B两点之间的距离AB=__________,线段AB的中点表示的数为_______;
②用含t的代数式表示:t秒后,点P表示的数为_______;点Q表示的数为_____.
(2) 求当t为何值时,P、Q 两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点 P在运动过程中,线段MN的长度是否发 生变化?若变化,请说明理由;若不变,请求出线段MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如下表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.
时间t(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
日销售量 | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
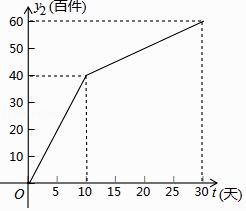
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映y1与t的变化规律,并求出y1与t的函数关系式及自变量t的取值范围;
(2)求y2与t的函数关系式,并写出自变量t的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为y(百件),求y与t的函数关系式;当t为何值时,日销售总量y达到最大,并求出此时的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,双曲线y=![]() (x>0)与直线y=kx-k的交点为点A(m,2).
(x>0)与直线y=kx-k的交点为点A(m,2).
(1) 求k的值;
(2) 当x>0时,直接写出不等式kx-k ≤![]() 的解集:_ ;
的解集:_ ;
(3) 设直线y=kx-k与y轴交于点B,若C是x轴上一点,且满足△ABC的面积是4,求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,高速公路的同一侧有A、B两城镇,它们到高速公路所在直线MN的距离分别为AA′=2 km,BB′=4 km,且A′B′=8 km.
(1)要在高速公路上A′、B′之间建一个出口P,使A、B两城镇到P的距离之和最小.请在图中画出P的位置,并作简单说明.
(2)求这个最短距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0,每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比,经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12),符合关系式x=2n2﹣2kn+9(k+3)(k为常数),且得到了表中的数据.
月份n(月) | 1 | 2 |
成本y(万元/件) | 11 | 12 |
需求量x(件/月) | 120 | 100 |
(1)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(2)求k,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第m个月和第(m+1)个月的利润相差最大,求m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com