
【题目】某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0,每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比,经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12),符合关系式x=2n2﹣2kn+9(k+3)(k为常数),且得到了表中的数据.
月份n(月) | 1 | 2 |
成本y(万元/件) | 11 | 12 |
需求量x(件/月) | 120 | 100 |
(1)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(2)求k,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第m个月和第(m+1)个月的利润相差最大,求m.
【答案】
(1)解:由题意,设y=a+ ![]() ,
,
由表中数据可得:  ,解得:
,解得: ![]() ,
,
∴y=6+ ![]() ,
,
由题意,若12=18﹣(6+ ![]() ),则
),则 ![]() =0,
=0,
∵x>0,
∴ ![]() >0,
>0,
∴不可能
(2)解:将n=1、x=120代入x=2n2﹣2kn+9(k+3),得:120=2﹣2k+9k+27,
解得:k=13,
∴x=2n2﹣26n+144,
将n=2、x=100代入x=2n2﹣26n+144也符合,
∴k=13;
由题意,得:18=6+ ![]() ,
,
解得:x=50,
∴50=2n2﹣26n+144,即n2﹣13n+47=0,
∵△=(﹣13)2﹣4×1×47<0,
∴方程无实数根,
∴不存在
(3)解:第m个月的利润为W,
W=x(18﹣y)=18x﹣x(6+ ![]() )
)
=12(x﹣50)
=24(m2﹣13m+47),
∴第(m+1)个月的利润为W′=24[(m+1)2﹣13(m+1)+47]=24(m2﹣11m+35),
若W≥W′,W﹣W′=48(6﹣m),m取最小1,W﹣W′取得最大值240;
若W<W′,W﹣W′=48(m﹣6),由m+1≤12知m取最大11,W﹣W′取得最大值240;
∴m=1或11
【解析】(1)设y=a+ ![]() ,将表中相关数据代入可求得a、b,根据12=18﹣(6+
,将表中相关数据代入可求得a、b,根据12=18﹣(6+ ![]() ),则
),则 ![]() =0可作出判断;(2)将n=1、x=120代入x=2n2﹣2kn+9(k+3)可求得k的值,先由18=6+
=0可作出判断;(2)将n=1、x=120代入x=2n2﹣2kn+9(k+3)可求得k的值,先由18=6+ ![]() 求得x=50,根据50=2n2﹣26n+144可判断;(3)第m个月的利润W=x(18﹣y)=18x﹣x(6+
求得x=50,根据50=2n2﹣26n+144可判断;(3)第m个月的利润W=x(18﹣y)=18x﹣x(6+ ![]() )=24(m2﹣13m+47),第(m+1)个月的利润为W′=24[(m+1)2﹣13(m+1)+47]=24(m2﹣11m+35),分情况作差结合m的范围,由一次函数性质可得.
)=24(m2﹣13m+47),第(m+1)个月的利润为W′=24[(m+1)2﹣13(m+1)+47]=24(m2﹣11m+35),分情况作差结合m的范围,由一次函数性质可得.


科目:初中数学 来源: 题型:
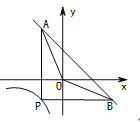
【题目】如图,P为反比例函数![]() (x<0)在第三象限内图象上的一点,过点P分别作x轴、y轴的垂线交一次函数y=-x+4的图像于点A、B.若AO、BO分别平分∠BAP,∠ABP ,则k的值为___________.
(x<0)在第三象限内图象上的一点,过点P分别作x轴、y轴的垂线交一次函数y=-x+4的图像于点A、B.若AO、BO分别平分∠BAP,∠ABP ,则k的值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
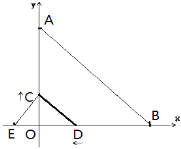
【题目】如图,已知点A(0,8)、B(8,0)、E(-2,0),动点 C从原点O出发沿OA方向以每秒1个单位长度向点A运动,动点D从点B出发沿BO方向以每秒2个单位长度向点O运动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动,设运动时间为t 秒。
(1)填空:直线AB的解析式是_____________________;
(2)求t的值,使得直线CD∥AB;
(3)是否存在时刻t,使得△ECD是等腰三角形?若存在,请求出一个这样的t值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1,因此,min{﹣ ![]() ,﹣
,﹣ ![]() }=;若min{(x﹣1)2 , x2}=1,则x= .
}=;若min{(x﹣1)2 , x2}=1,则x= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=4,AD=5,E为射线BC上一点,DF⊥AE于F,连结DE.
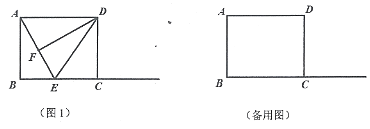
(1)当E在线段BC上时
①若DE=5,求BE的长;
②若CE=EF,求证:AD=AE;
(2)连结BF,在点E的运动过程中:
①当△ABF是以AB为底的等腰三角形时,求BE的长;
②记△ADF的面积为S1,记△DCE的面积为S2,当BF∥DE时,请直接写出S1:S2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题: ①若AC=AB,则DE=CE;
②若∠C=45°,记△CDE的面积为S1 , 四边形DABE的面积为S2 , 则S1=S2 ,
那么( )
A.①是真命题②是假命题
B.①是假命题②是真命题
C.①是假命题②是假命题
D.①是真命题②是真命题
查看答案和解析>>
科目:初中数学 来源: 题型:
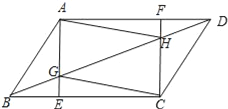
【题目】已知:如图,在ABCD中,AE⊥BC,CF⊥AD,垂足分别为E、F,AE、CF分别与BD相交于点G、H,联结AH、CG.
求证:四边形AGCH是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
①AE=BF;②AE⊥BF;③sin∠BQP= ![]() ;④S四边形ECFG=2S△BGE .
;④S四边形ECFG=2S△BGE . 
A.4
B.3
C.2
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com