
����Ŀ��������֪ʶ�������dz�����ѧ��һ����Ҫ���ߣ�����������Խ������������ؽ� ��.�о��������Ƿ�����������Ҫ�Ĺ��ɣ��������ϵ� A���� B ��ʾ�����ֱ�Ϊ a��b����A��B ����֮��ľ��� AB= ![]() ���߶� AB ���е��ʾ����Ϊ
���߶� AB ���е��ʾ����Ϊ![]() .
.
�������龳����ͼ�������ϵ�A��ʾ����Ϊ-2����B��ʾ����Ϊ8����P�ӵ� A ������ ��ÿ��3����λ���ȵ��ٶ����������������˶���ͬʱ��Q�ӵ�B��������ÿ�� 2���� λ���ȵ��ٶ����������˶������˶�ʱ��Ϊt��(t��0).
���ۺ����á�(1) ��գ�
��A��B����֮��ľ���AB=__________���߶�AB���е��ʾ����Ϊ_______��
���ú�t�Ĵ���ʽ��ʾ��t���P��ʾ����Ϊ_______����Q��ʾ����Ϊ_____.
(2) ��tΪ��ֵʱ��P��Q ������������д������������ʾ������
(3)��tΪ��ֵʱ��PQ=![]() AB��
AB��
(4)����MΪPA���е㣬��NΪPB���е㣬�� P���˶������У��߶�MN�ij����Ƿ� ���仯�����仯����˵�����ɣ������䣬������߶�MN�ij�.

���𰸡���1����10��3����-2+3t��8-2t����2����t=2ʱ��P��Q�������������ʾ����Ϊ4����3��t=1��3����4��5.
�������������������1���������⼴�ɵõ����ۣ�
��2����P��Q��������ʱ��P��Q��ʾ��������з��̵õ�t=2�����ǵõ���t=2ʱ��P��Q���������ɵõ����ۣ�
��3����t���P��ʾ������2+3t����Q��ʾ����Ϊ8��2t�����ǵõ�PQ=|����2+3t������8��2t��|=|5t��10|���з��̼��ɵõ����ۣ�
��4���ɵ�M��ʾ����Ϊ ![]() ����N��ʾ����Ϊ
����N��ʾ����Ϊ![]() �����ɵõ����ۣ�
�����ɵõ����ۣ�
����������⣺��1����10��3��
�ک�2+3t��8��2t��
��2������P��Q��������ʱ��P��Q��ʾ����������ੁ2+3t=8��2t����ã�t=2������t=2ʱ��P��Q��������ʱ����2+3t=��2+3��2=4�����������ʾ����Ϊ4��
��3����t���P��ʾ������2+3t����Q��ʾ����Ϊ8��2t����PQ=|����2+3t������8��2t��|=|5t��10|����PQ=![]() AB=
AB=![]() ��10=5����|5t��10|=5����ã�t=1��3��
��10=5����|5t��10|=5����ã�t=1��3��
������t=1��3ʱ��PQ=![]() AB��
AB��
��4������M��ʾ����Ϊ ![]() ����N��ʾ����Ϊ
����N��ʾ����Ϊ ![]() ����MN=|��
����MN=|��![]() ������
������![]() ��|=|
��|=|![]() |=5��
|=5��


 �����ߴ���ϵ�д�
�����ߴ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����DAB=��CAE��Ҫʹ��ABC�ס�ADE�����һ��������������ע��ֻ��д��һ����ȷ�𰸼��ɣ��� 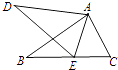
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������CD��AB�ڵ�H����G�ڻ�BD�ϣ�����AG����CD�ڵ�K������G��ֱ�߽�CD�ӳ����ڵ�E����AB�ӳ����ڵ�F����EG=EK�� 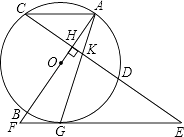
��1����֤��EF�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ13��CH=12��AC��EF����OH��FG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
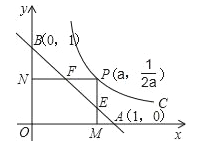
����Ŀ����ͼ����֪����P�ں���![]() ��x��0����ͼ�����˶���PM��x���ڵ�M��PN��y���ڵ�N���߶�PM��PN�ֱ���ֱ��AB��y=��x+1���ڵ�E��F����AFBE��ֵΪ��������
��x��0����ͼ�����˶���PM��x���ڵ�M��PN��y���ڵ�N���߶�PM��PN�ֱ���ֱ��AB��y=��x+1���ڵ�E��F����AFBE��ֵΪ��������
A. 4 B. 2 C. 1 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У�����ȷ���ǣ� ��
A. ƽ�����ڱ�������ֻ��![]() ��
��![]() B. �����ľ���ֵ���������������ľ���ֵ�������෴��
B. �����ľ���ֵ���������������ľ���ֵ�������෴��
C. �������IJ�Ϊ����������������һ������ D. ��������������ֵ��ĸ�������С
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿ�����Լ��ˮ��ʶ��ij����2018�꿪ʼ�Թ�ˮ��Χ�ڵľ�����ˮʵ�С������շѡ��������շѱ����±���

ij���������·���ˮ10 m3ʱ������ˮ��23Ԫ��
(1) ��a��ֵ��
(2) ���û��������·�����ˮ��Ϊ71Ԫ����û��������·ݵ���ˮ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������480 t�Ĵ����ݻ���1050 m3�����м��ֻ���450 m3�����ֻ���350 t�������ֻ���ÿ�����2��5 m3�����ֻ���ÿ������0��5 t�������ֻ����Ƿ���װ�ϴ�? ������ܣ���˵�����ɣ������Ϊ������ȵ����ô������������ݻ������ֻ���Ӧ��װ���ٶ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����б�߳�Ϊ4��ֱ�����ǰ����ֱ������ϵxOy�У�����ֱ�DZ߷ֱ����������غϣ�PΪб�ߵ��е㣮�ֽ������ǰ��Ƶ�O˳ʱ����ת120����P�Ķ�Ӧ��������ǣ� ��
A.�� ![]() ��1��
��1��
B.��1���� ![]() ��
��
C.��2 ![]() ����2��
����2��
D.��2����2 ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧ�ڵ���ѧ����ɼ������ʾ��
���� ��� | ƽʱ���� | ���� ���� | ��ĩ ���� | |||
��1�� | ��2�� | ��3�� | ��4�� | |||
�ɼ� | 80 | 86 | 84 | 90 | 90 | 95 |
(1)�����β���ɼ�����������λ����
(2)��С����ѧ�ڵ���ѧƽʱ�����ƽ���ɼ���
(3)�����ѧ�ڵ������ɼ��ǽ�ƽʱ�����ƽ���ɼ������в���ɼ�����ĩ����ɼ�����3:3:4�ı����������ã�����С����ѧ��ѧ�Ƶ������ɼ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com