
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点H,点G在弧BD上,连接AG,交CD于点K,过点G的直线交CD延长线于点E,交AB延长线于点F,且EG=EK. 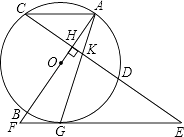
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为13,CH=12,AC∥EF,求OH和FG的长.
【答案】
(1)证明:连接OG,
∵弦CD⊥AB于点H,
∴∠AHK=90°,
∴∠HKA+∠KAH=90°,
∵EG=EK,
∴∠EGK=∠EKG,
∵∠HKA=∠GKE,
∴∠HAK+∠KGE=90°,
∵AO=GO,
∴∠OAG=∠OGA,
∴∠OGA+∠KGE=90°,
∴GO⊥EF,
∴EF是⊙O的切线
(2)解:连接CO,在Rt△OHC中,
∵CO=13,CH=12,
∴HO=5,
∴AH=8,
∵AC∥EF,
∴∠CAH=∠F,
∴tan∠CAH=tan∠F= ![]() =
= ![]() ,
,
在Rt△OGF中,∵GO=13,
∴FG= ![]() =
= ![]() .
.
【解析】(1)连接OG,首先证明∠EGK=∠EKG,再证明∠HAK+∠KGE=90°,进而得到∠OGA+∠KGE=90°即GO⊥EF,进而证明EF是⊙O的切线;(2)连接CO,利用勾股定理计算出HO的长,然后可得tan∠CAH=tan∠F= ![]() =
= ![]() ,再利用三角函数在Rt△OGF中计算出FG的长.
,再利用三角函数在Rt△OGF中计算出FG的长.
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


科目:初中数学 来源: 题型:
【题目】射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心, ![]() cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值(单位:秒)
cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值(单位:秒) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
(1)如图①,当直线l与⊙O相切于点C时,求证:AC平分∠DAB; 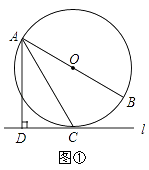
(2)如图②,当直线l与⊙O相交于点E,F时,求证:∠DAE=∠BAF. 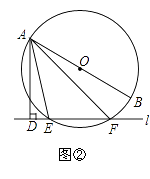
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )

A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△ CED D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
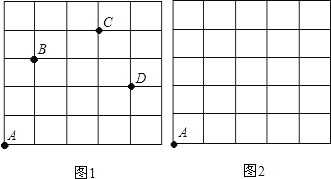
【题目】如图,一只甲虫在5![]() 5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为:
5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为:![]() (+1,+3);从C到D 记为:
(+1,+3);从C到D 记为:![]() (+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.
(+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.
(1)填空:![]() 记为( , ),
记为( , ), ![]() 记为( , );
记为( , );
(2)若甲虫的行走路线为:![]() ,请你计算甲虫走过的路程.
,请你计算甲虫走过的路程.
(3)若这只甲虫去Q的行走路线依次为:A→M(+2,+2),M→N(+2,-1),N→P(-2,+3),P→Q(-1,-2),请依次在图2标出点M、N、P、Q的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结 合.研究数轴我们发现了许多重要的规律:若数轴上点 A、点 B 表示的数分别为 a、b,则A、B 两点之间的距离 AB= ![]() ,线段 AB 的中点表示的数为
,线段 AB 的中点表示的数为![]() .
.
【问题情境】如图,数轴上点A表示的数为-2,点B表示的数为8,点P从点 A 出发, 以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒 2个单 位长度的速度向左匀速运动,设运动时间为t秒(t>0).
【综合运用】(1) 填空:
①A、B两点之间的距离AB=__________,线段AB的中点表示的数为_______;
②用含t的代数式表示:t秒后,点P表示的数为_______;点Q表示的数为_____.
(2) 求当t为何值时,P、Q 两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点 P在运动过程中,线段MN的长度是否发 生变化?若变化,请说明理由;若不变,请求出线段MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA.
(1)求证:∠BAD=∠EDC;
(2)作出点E关于直线BC的对称点M,连接DM、AM,猜想DM与AM的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com