
【题目】已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
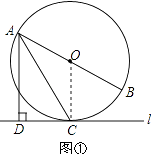
(1)如图①,当直线l与⊙O相切于点C时,求证:AC平分∠DAB; 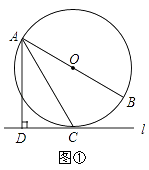
(2)如图②,当直线l与⊙O相交于点E,F时,求证:∠DAE=∠BAF. 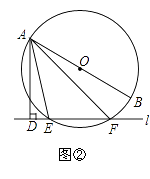
【答案】
(1)证明:连接OC,
∵直线l与⊙O相切于点C,
∴OC⊥CD;
又∵AD⊥CD,
∴AD∥OC,
∴∠DAC=∠ACO;
又∵OA=OC,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
即AC平分∠DAB
(2)证明:如图②,连接BF,
∵AB是⊙O的直径,
∴∠AFB=90°,
∴∠BAF=90°﹣∠B,
∴∠AEF=∠ADE+∠DAE,
在⊙O中,四边形ABFE是圆的内接四边形,
∴∠AEF+∠B=180°,
∴∠BAF=∠DAE
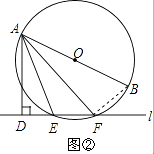
【解析】(1)连接OC,易得OC∥AD,根据平行线的性质就可以得到∠DAC=∠ACO,再根据OA=OC得到∠ACO=∠CAO,就可以证出结论;(2)如图②,连接BF,由AB是⊙O的直径,根据直径所对的圆周角是直角,可得∠AFB=90°,由三角形外角的性质,可求得∠AEF的度数,又由圆的内接四边形的性质,继而证得结论.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )

A. ①②④ B. ②③④
C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形 ABCD 中, AB = a, BC = b, a > b .以 AB 边为轴将长方形旋转一周形成 圆柱体甲,再以 BC 边为轴将长方形旋转一周形成圆柱体乙.记两个圆柱体的体积分别为 V甲 ,V乙 ,侧面积分别为 S甲, S乙 ,则下列正确的是( )
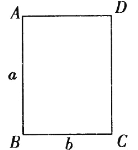
A. V甲 > V乙 , S甲=S乙
B. V甲 < V乙 , S甲= S乙
C. V甲= V乙 , S甲= S乙
D. V甲 > V乙 , S甲 < S乙
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一种牛奶软包装盒如图1所示.为了生产这种包装盒,需要先画出展开图纸样.
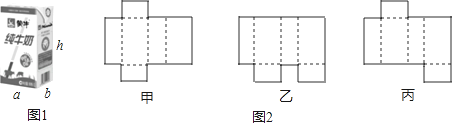
(1)如图2给出三种纸样甲.乙.丙,在甲.乙.丙中,正确的有________.
(2)从已知正确的纸样中选出一种,在原图上标注上尺寸.
(3)利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和)
查看答案和解析>>
科目:初中数学 来源: 题型:
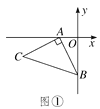
【题目】如图①,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC.
(1)求C点的坐标;
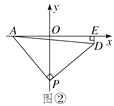
(2)如图②,OA=2,P为y轴负半轴上一个动点,当P点在y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OP-DE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点H,点G在弧BD上,连接AG,交CD于点K,过点G的直线交CD延长线于点E,交AB延长线于点F,且EG=EK. 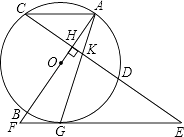
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为13,CH=12,AC∥EF,求OH和FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
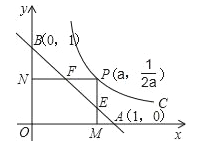
【题目】如图,已知动点P在函数![]() (x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AFBE的值为( )
(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AFBE的值为( )
A. 4 B. 2 C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )
A.( ![]() ,1)
,1)
B.(1,﹣ ![]() )
)
C.(2 ![]() ,﹣2)
,﹣2)
D.(2,﹣2 ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com