
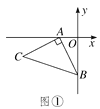
【题目】如图①,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC.
(1)求C点的坐标;
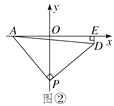
(2)如图②,OA=2,P为y轴负半轴上一个动点,当P点在y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OP-DE的值.
【答案】(1)点C的坐标为(-6,-2);(2)OP-DE=2.
【解析】(1)如图1,过C作CM⊥x轴于M点,则可以求出△MAC≌△OBA,可得CM=OA=2,MA=OB=4,故点C的坐标为(-6,-2).
(2)如图2,过D作DQ⊥OP于Q点,则DE=OQ利用三角形全等的判定定理可得△AOP≌△PQD(AAS)进一步可得PQ=OA=2,即OP-DE=2.
(1)如图①,过C作CM⊥x轴于M点,
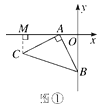
则∠CMA=90°.
∵△ABC为等腰直角三角形,且∠AOB=90°,
∴∠BAC=90°,AC=BA,
∴∠MAC+∠OAB=90°,∠OAB+∠OBA=90°,则∠MAC=∠OBA.
在△MAC和△OBA中,
∠CMA=∠AOB,∠MAC=∠OBA,AC=BA,
∴△MAC≌△OBA(AAS),
∴CM=OA=2,MA=OB=4,
∴OM=OA+AM=2+4=6,
∴点C的坐标为(-6,-2).
(2)如图②,过D作DQ⊥OP于Q点,
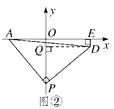
则∠PQD=90°,DE=OQ,
∴OP-DE=OP-OQ=PQ.
∵△APD为等腰直角三角形,且∠AOP=90°,
∴∠APD=90°,AP=PD,∴∠APO+∠QPD=90°,∠APO+∠OAP=90°,
∴∠QPD=∠OAP.
在△AOP和△PQD中,
∠AOP=∠PQD,∠QPD=∠OAP,AP=PD,
∴△AOP≌△PQD(AAS).
∴PQ=OA=2.即OP-DE=2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:在数学课上,老师提出如下问题:
尺规作图,过圆外一点作圆的切线. |
小涵的主要作法如下:
如图,(1)连结OP,作线段OP的中点A; |
老师说:“小涵的做法是正确的.”
请回答:小涵的作图依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点F.请你添加一个适当的条件,使△AEF≌△CEB.添加的条件是____________(写出一个即可).
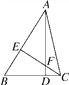
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从图 2 开始,每一个图形都是由基本图形“△”通过平移或翻折拼成的:

观察发现,图 10 中共有_________________个小三角形,图 n 共有____________个小三角形,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
(1)如图①,当直线l与⊙O相切于点C时,求证:AC平分∠DAB; 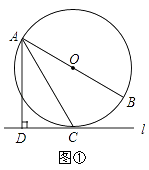
(2)如图②,当直线l与⊙O相交于点E,F时,求证:∠DAE=∠BAF. 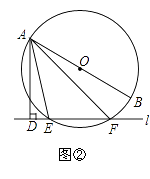
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )

A. ①②④ B. ②③④
C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y= ![]() x2﹣3x+4,
x2﹣3x+4,
(1)配方成y=a(x﹣h)2+k的形式.
(2)求出它的图象的顶点坐标和对称轴.
(3)求出函数的最大或最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2﹣4ac>0;④a+b+c<0;⑤4a﹣2b+c<0,其中正确的个数是( ) 
A.2
B.3
C.4
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com