
【题目】对于二次函数y= ![]() x2﹣3x+4,
x2﹣3x+4,
(1)配方成y=a(x﹣h)2+k的形式.
(2)求出它的图象的顶点坐标和对称轴.
(3)求出函数的最大或最小值.
【答案】
(1)解:y= ![]() x2﹣3x+4
x2﹣3x+4
= ![]() (x2﹣6x)+4
(x2﹣6x)+4
= ![]() [(x﹣3)2﹣9]+4
[(x﹣3)2﹣9]+4
= ![]() (x﹣3)2﹣
(x﹣3)2﹣ ![]()
(2)解:由(1)得:图象的顶点坐标为:(3,﹣ ![]() ),
),
对称轴为:直线x=3
(3)解:∵a= ![]() >0,
>0,
∴函数的最小值为:﹣ ![]()
【解析】(1)直接利用配方法求出二次函数的顶点式即可;(2)利用(1)中所求得出二次函数的顶点坐标和对称轴;(3)利用(1)中所求得出二次函数的最值.
【考点精析】根据题目的已知条件,利用二次函数的最值的相关知识可以得到问题的答案,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】近两年,国际市场黄金价格涨幅较大,中国交通银行推出“沃德金”的理财产品,即以黄金为投资产品,投资者从黄金价格的上涨中赚取利润.上周五黄金的收盘价为![]() 元/克,下表是本周星期一至星期五黄金价格的变化情况.(注:星期一至星期五开市,星期六、星期日休市)
元/克,下表是本周星期一至星期五黄金价格的变化情况.(注:星期一至星期五开市,星期六、星期日休市)
星期 | 一 | 二 | 三 | 四 | 五 |
收盘价的变化(与前一天收盘价比较) |
|
|
|
|
|
问
![]() 本周星期三黄金的收盘价是多少?
本周星期三黄金的收盘价是多少?
![]() 本周黄金收盘时的最高价、最低价分别是多少?
本周黄金收盘时的最高价、最低价分别是多少?
![]() 上周,小王以周五的收盘价
上周,小王以周五的收盘价![]() 元/克买入黄金
元/克买入黄金![]() 克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金
克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金![]() 克,他的收益情况如何?
克,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
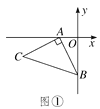
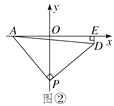
【题目】如图①,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC.
(1)求C点的坐标;
(2)如图②,OA=2,P为y轴负半轴上一个动点,当P点在y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OP-DE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=ax2﹣2(a﹣1)x+a﹣2(a>0).
(1)求证:抛物线与x轴有两个交点;
(2)设抛物线与x轴有两个交点的横坐标分别为x1 , x2 , (其中x1>x2).若y是关于a的函数,且y=ax2+x1 , 求这个函数的表达式;
(3)在(2)的条件下,结合函数的图象回答:若使y≤﹣3a2+1,则自变量a的取值范围为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
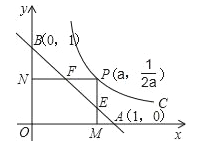
【题目】如图,已知动点P在函数![]() (x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AFBE的值为( )
(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AFBE的值为( )
A. 4 B. 2 C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论:w
①若a+b+c=0,且abc≠0,则方程a+bx+c=0的解是x=1;
②若a(x﹣1)=b(x﹣1)有唯一的解,则a≠b;
③若b=2a,则关于x的方程ax+b=0(a≠0)的解为x=﹣![]() ;
;
④若a+b+c=1,且a≠0,则x=1一定是方程ax+b+c=1的解;
其中结论正确个数有( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强居民节约用水意识,某市在2018年开始对供水范围内的居民用水实行“阶梯收费”,具体收费标准如下表:

某户居民四月份用水10 m3时,缴纳水费23元.
(1) 求a的值;
(2) 若该户居民五月份所缴水费为71元,求该户居民五月份的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=2AD, AH⊥BC于点H,E是CD的中点,连接AE、 BE、HE.
(1)求证: AE⊥BE
(2)求证:∠DEH=3 ∠ EHC

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=5,AB的垂直平分线DE分别交AB,AC于E,D.
(1)若△BCD的周长为8,求BC的长;
(2)若BC=4,求△BCD的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com