
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c>0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0; 其中正确的个数为( )
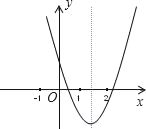
A. 1个 B. 2个 C. 3个 D. 4个
【答案】A
【解析】
由抛物线开口向上得到a大于0,再由对称轴在y轴右侧得到a与b异号,即b小于0,由抛物线与y轴交于正半轴,得到c大于0,可得出abc的符合,对于(3)作出判断;由x=1时对应的函数值小于0,将x=1代入二次函数解析式得到a+b+c小于0,(1)错误;根据对称轴在1和2之间,利用对称轴公式列出不等式,由a大于0,得到-2a小于0,在不等式两边同时乘以-2a,不等号方向改变,可得出不等式,对(2)作出判断;由x=-1时对应的函数值大于0,将x=-1代入二次函数解析式得到a-b+c大于0,又4a大于0,c大于0,可得出a-b+c+4a+c大于0,合并后得到(4)正确,综上,即可得到正确的个数.
由图形可知:抛物线开口向上,与y轴交点在正半轴,
∴a>0,b<0,c>0,即abc<0,故(3)错误;
又x=1时,对应的函数值小于0,故将x=1代入得:a+b+c<0,故(1)错误;
∵对称轴在1和2之间,
∴![]() 又a>0,
又a>0,
∴在不等式左右两边都乘以2a得:2a>b>4a,故(2)正确;
又x=1时,对应的函数值大于0,故将x=1代入得:ab+c>0,
又a>0,即4a>0,c>0,
∴5ab+2c=(ab+c)+4a+c>0,故(4)错误,
综上,正确的有1个,为选项(2).
故选:A.


科目:初中数学 来源: 题型:
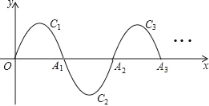
【题目】如图,一段抛物线y=﹣x(x﹣4)(0≤x≤4),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(2015,m)在此“波浪线”上,则m的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
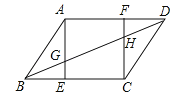
【题目】如图,在平行四边形ABCD中,AE⊥BC,CF⊥AD,垂足分别为E,F,AE,CF分别与BD交于点G和H,且AB=![]() .
.
(1)若tan∠ABE =2,求CF的长;
(2)求证:BG=DH.
查看答案和解析>>
科目:初中数学 来源: 题型:
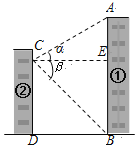
【题目】(8分)某中学九年级学生在学习“直角三角形的边角关系”时,组织开展测量物体高度的实践活动.在活动中,某小组为了测量校园内①号楼AB的高度(如图),站在②号楼的C处,测得①号楼顶部A的仰角α=30°,底部B的俯角β=45°.已知两幢楼的水平距离BD为18米,求①号楼AB的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一块含30°角的直角三角板OAB和一块等腰直角三角板ODC按如图的方式放置在平面直角坐标系中.已知C、B两点分别在x轴和y轴上,∠ABO=∠D=90°,OB=OC,AB=3.
(1)求边OC的长.
(2)将直角三角板OAB绕点顺时针方向旋转,使OA落在x轴上的OA′位置,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)如图![]() ,
,![]() 中,
中,![]() ,
,![]() ,我们可以利用
,我们可以利用![]() 与
与![]() 相似证明
相似证明![]() ,这个结论我们称之为射影定理,试证明这个定理;
,这个结论我们称之为射影定理,试证明这个定理;
(结论运用)如图![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 是对角线
是对角线![]() 、
、![]() 的交点,点
的交点,点![]() 在
在![]() 上,过点
上,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,
(1)试利用射影定理证明![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
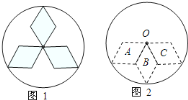
【题目】如图![]() 所示,某产品的标志图案,要在所给的图形图
所示,某产品的标志图案,要在所给的图形图![]() 中,把
中,把![]() ,
,![]() ,
,![]() 三个菱形通过一种或几种变换,使之变为与图
三个菱形通过一种或几种变换,使之变为与图![]() 一样的图案:
一样的图案:
(1)请你在图![]() 中作出变换后的图案(最终图案用实线表示);
中作出变换后的图案(最终图案用实线表示);
(2)你所用的变换方法是________(在以下变换方法中,选择一种正
确的填到横线上,也可以用自己的话表述).
①将菱形![]() 向上平移;
向上平移;
②将菱形![]() 绕点
绕点![]() 旋转
旋转![]() ;
;
③将菱形![]() 绕点
绕点![]() 旋转
旋转![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代有着辉煌的数学成就,《周牌算经》、《九章算术》、《海岛算经》、《孙子算经》等是我国古代数学的重要文献.
(1)小聪想从这4部数学名著中随机选择1部阅读,求他选中《九章算术》的概率;
(2)小聪拟从这4部数学名著中选择2部作为假课外拓展学习内容,用列表或树状图求选中的名著恰好是《九章算术》和《周牌算经》的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com