
【题目】(问题情境)如图![]() ,
,![]() 中,
中,![]() ,
,![]() ,我们可以利用
,我们可以利用![]() 与
与![]() 相似证明
相似证明![]() ,这个结论我们称之为射影定理,试证明这个定理;
,这个结论我们称之为射影定理,试证明这个定理;
(结论运用)如图![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 是对角线
是对角线![]() 、
、![]() 的交点,点
的交点,点![]() 在
在![]() 上,过点
上,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,
(1)试利用射影定理证明![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.

【答案】【问题情境】证明见解析;【结论运用】![]() 证明见解析;(2)
证明见解析;(2)![]() .
.
【解析】
通过证明Rt△ACD∽Rt△ABC得到AC:AB=AD:AC,然后利用比例性质即可得到AC2=ADAB;
【结论运用】
(1)根据射影定理得BC2=BOBD,BC2=BFBE,则BOBD=BFBE,即![]() =
=![]() ,加上∠OBF=∠EBD,于是可根据相似三角形的判定得到△BOF∽△BED;
,加上∠OBF=∠EBD,于是可根据相似三角形的判定得到△BOF∽△BED;
(2)先计算出DE=4,CE=2,BE=2![]() ,OB=3
,OB=3![]() ,再利用(1)中结论△BOF∽△BED得到
,再利用(1)中结论△BOF∽△BED得到![]() =
=![]() ,即
,即![]() =
=![]() ,然后利用比例性质求OF.
,然后利用比例性质求OF.
如图1.
∵CD⊥AB,∴∠ADC=90°,而∠CAD=∠BAC,∴Rt△ACD∽Rt△ABC,∴AC:AB=AD:AC,∴AC2=ADAB;
(1)如图2.
∵四边形ABCD为正方形,∴OC⊥BO,∠BCD=90°,∴BC2=BOBD.
∵CF⊥BE,∴BC2=BFBE,∴BOBD=BFBE,即![]() =
=![]() ,而∠OBF=∠EBD,∴△BOF∽△BED;
,而∠OBF=∠EBD,∴△BOF∽△BED;
(2)∵BC=CD=6,而DE=CE,∴DE=4,CE=2.
在Rt△BCE中,BE=![]() =2
=2![]() .在Rt△OBC中,OB=
.在Rt△OBC中,OB=![]() BC=3
BC=3![]() .
.
∵△BOF∽△BED,∴![]() =
=![]() ,即
,即![]() =
=![]() ,∴OF=
,∴OF=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.
(1)求证:四边形AEDF是菱形;
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c>0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0; 其中正确的个数为( )
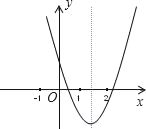
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AP是⊙O的切线,点A为切点,BP与⊙O交于点C,点D是AP的中点,连结CD.
(1)求证:CD是⊙O的切线;
(2)若AB=2,∠P=30°,求阴影部分的面积.
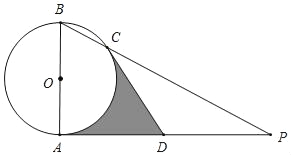
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将某种商品的售价从原来的每件![]() 元经两次调价后调至每件
元经两次调价后调至每件![]() 元.
元.
(1)若该商店两次调价的降价率相同,求这个降价率;
(2)经调查,该商品每降价![]() 元,即可多销售
元,即可多销售![]() 件.若该商品原来每月可销售
件.若该商品原来每月可销售![]() 件,那么两次调价后,每月可销售该商品多少件?
件,那么两次调价后,每月可销售该商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年4月23日是世界读书日,某校为了解学生课外阅读情况,随机抽取20名学生,对每人每周用于课外阅读的平均时间(单位:min)进行调查,过程如下:
收集数据:
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据:
课外阅读平均时间x(min) | 0≤x<40 | 40≤x<80 | 80≤x<120 | 120≤x<160 |
等级 | D | C | B | A |
人数 | 3 | a | 8 | b |
分析数据:
平均数 | 中位数 | 众数 |
80 | m | n |
请根据以上提供的信息,解答下列问题:
(1)填空:a= ,b= ;m= ,n= ;
(2)已知该校学生500人,若每人每周用于课外阅读的平均时间不少于80min为达标,请估计达标的学生数;
(3)设阅读一本课外书的平均时间为260min,请选择适当的统计量,估计该校学生每人一年(按52周计)平均阅读多少本课外书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A(m,n)为直线y=-x+4上一动点,且满足-4<m<4,将O点绕点B![]() 逆时针旋转90°得点C,连接AC,则线段AC长度的取值范围是____________.
逆时针旋转90°得点C,连接AC,则线段AC长度的取值范围是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
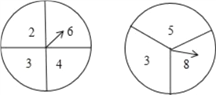
【题目】初三年(4)班要举行一场毕业联欢会,主持人同时转动下图中的两个转盘,由一名同学在转动前来判断两个转盘上指针所指的两个数字之和是奇数还是偶数,如果判断错误,他就要为大家表演一个节目;如果判断正确,他可以指派别人替自己表演节目.现在轮到小明来选择,小明不想自己表演,于是他选择了偶数.
小明的选择合理吗?从概率的角度进行分析(要求用树状图或列表方法求解)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com