
【题目】点A(m,n)为直线y=-x+4上一动点,且满足-4<m<4,将O点绕点B![]() 逆时针旋转90°得点C,连接AC,则线段AC长度的取值范围是____________.
逆时针旋转90°得点C,连接AC,则线段AC长度的取值范围是____________.
【答案】2![]() ≤AC<10
≤AC<10![]() .
.
【解析】
首先证明点A在运动过程中,△ABC的形状相同,推出AB的值最大时,AC的值最大,AB的值最小时,AC的值最小,结合图形分别求出AB的最大值,最小值即可解决问题.
如图1中,

∵A(m,n),
∴点A关于原点对称点A′(-m,-n),
∴OA′的中点B(-![]() ,-
,-![]() );
);
∴OA=2OB=2BC,
∴tan∠CAB=![]() ,
,
∴点A在运动过程中,△ABC的形状相同,
∴AB的值最大时,AC的值最大,AB的值最小时,AC的值最小,
当点A的坐标为(-4,8)时,AB的值最大,
此时B(2,-4),
∴AB=![]() ,
,
∴BC=![]() AB=2
AB=2![]() ,
,
∴AC=![]() .
.
如图2中,当直线AB⊥直线y=-x+4时,AB的值最小,此时直线AB的解析式为y=x,
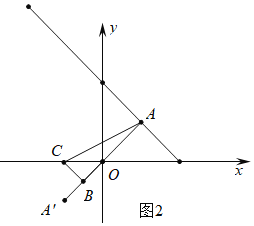
由![]() ,
,
解得![]() ,
,
∴A(2,2),B(-1,-1),
∴AB=![]() ,
,
∴BC=![]() AB=
AB=![]() ,
,
∴AC=![]() ,
,
综上所述,线段AC长度的取值范围是2![]() ≤AC<10
≤AC<10![]() ,
,
故答案为2![]() ≤AC<10
≤AC<10![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)如图![]() ,
,![]() 中,
中,![]() ,
,![]() ,我们可以利用
,我们可以利用![]() 与
与![]() 相似证明
相似证明![]() ,这个结论我们称之为射影定理,试证明这个定理;
,这个结论我们称之为射影定理,试证明这个定理;
(结论运用)如图![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 是对角线
是对角线![]() 、
、![]() 的交点,点
的交点,点![]() 在
在![]() 上,过点
上,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,
(1)试利用射影定理证明![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 所示,某产品的标志图案,要在所给的图形图
所示,某产品的标志图案,要在所给的图形图![]() 中,把
中,把![]() ,
,![]() ,
,![]() 三个菱形通过一种或几种变换,使之变为与图
三个菱形通过一种或几种变换,使之变为与图![]() 一样的图案:
一样的图案:
(1)请你在图![]() 中作出变换后的图案(最终图案用实线表示);
中作出变换后的图案(最终图案用实线表示);
(2)你所用的变换方法是________(在以下变换方法中,选择一种正
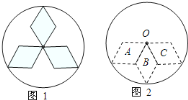
确的填到横线上,也可以用自己的话表述).
①将菱形![]() 向上平移;
向上平移;
②将菱形![]() 绕点
绕点![]() 旋转
旋转![]() ;
;
③将菱形![]() 绕点
绕点![]() 旋转
旋转![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,小明和爸爸去大剧院看电影.爸爸步行先走,小明在爸爸离开家一段时间后骑自行车去,两人按相同的路线前往大剧院,他们所走的路程![]() (米)和时间
(米)和时间![]() (分)的关系如图所示,则小明追上爸爸时,爸爸共走了_____________米.
(分)的关系如图所示,则小明追上爸爸时,爸爸共走了_____________米.
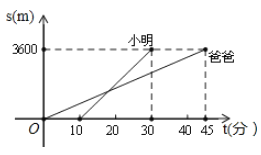
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人的某一人.
(1)求第二次传球后球回到甲手里的概率.
(2)如果甲跟另外n(n≥2)个人做(1)同样的游戏,那么,第三次传球后球回到甲手里的概率是 .(请用含n的式子直接写结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果方程x2+px+q=0的两个根是x1、x2,那么x1+x2=-p,x1·x2=q.请根据以上结论,解决下列问题:
(1)已知关于x的方程x2+mx+n=0 (n≠0),求出一个一元二次方程,使它的两根分别是已知方程两根的倒数;
(2)已知a、b满足a2-15a-5=0,b2-15b-5=0,求![]() 的值;
的值;
(3)已知a、b、c均为实数,且a+b+c=0,abc=16,求正数c的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代有着辉煌的数学成就,《周牌算经》、《九章算术》、《海岛算经》、《孙子算经》等是我国古代数学的重要文献.
(1)小聪想从这4部数学名著中随机选择1部阅读,求他选中《九章算术》的概率;
(2)小聪拟从这4部数学名著中选择2部作为假课外拓展学习内容,用列表或树状图求选中的名著恰好是《九章算术》和《周牌算经》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 、
、![]() 是弧
是弧![]() (异于
(异于![]() 、
、![]() )上两点,
)上两点,![]() 是弧
是弧![]() 上一动点,
上一动点,![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() .当点
.当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则
时,则![]() 、
、![]() 两点的运动路径长的比是( )
两点的运动路径长的比是( )
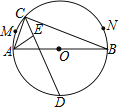
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com