
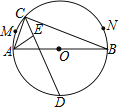
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 、
、![]() 是弧
是弧![]() (异于
(异于![]() 、
、![]() )上两点,
)上两点,![]() 是弧
是弧![]() 上一动点,
上一动点,![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() .当点
.当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则
时,则![]() 、
、![]() 两点的运动路径长的比是( )
两点的运动路径长的比是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
连接BE,由题意可得点E是△ABC的内心,由此可得∠AEB=135°,为定值,确定出点E的运动轨迹是是弓形AB上的圆弧,此圆弧所在圆的圆心在AB的中垂线上,根据题意过圆心O作直径CD,则CD⊥AB,在CD的延长线上,作DF=DA,则可判定A、E、B、F四点共圆,继而得出DE=DA=DF,点D为弓形AB所在圆的圆心,设⊙O的半径为R,求出点C的运动路径长为![]() ,DA=
,DA=![]() R,进而求出点E的运动路径为弧AEB,弧长为
R,进而求出点E的运动路径为弧AEB,弧长为![]() ,即可求得答案.
,即可求得答案.
连结BE,
∵点E是∠ACB与∠CAB的交点,
∴点E是△ABC的内心,
∴BE平分∠ABC,
∵AB为直径,
∴∠ACB=90°,
∴∠AEB=180°-![]() (∠CAB+∠CBA)=135°,为定值,
(∠CAB+∠CBA)=135°,为定值,![]() ,
,
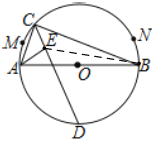
∴点E的轨迹是弓形AB上的圆弧,
∴此圆弧的圆心一定在弦AB的中垂线上,
∵![]() ,
,
∴AD=BD,
如下图,过圆心O作直径CD,则CD⊥AB,
∠BDO=∠ADO=45°,
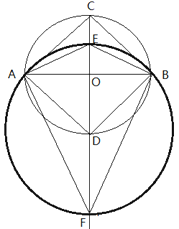
在CD的延长线上,作DF=DA,
则∠AFB=45°,
即∠AFB+∠AEB=180°,
∴A、E、B、F四点共圆,
∴∠DAE=∠DEA=67.5°,
∴DE=DA=DF,
∴点D为弓形AB所在圆的圆心,
设⊙O的半径为R,
则点C的运动路径长为:![]() ,
,
DA=![]() R,
R,
点E的运动路径为弧AEB,弧长为:![]() ,
,
C、E两点的运动路径长比为: ,
,
故选A.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】(本题满分8分)
为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动.学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:


请根据图表信息回答下列问题:
(1)频数分布表中的![]() ,
,![]() ;
;
(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在![]() 小时以上的学生评为“阅读之星”,请你估计该校
小时以上的学生评为“阅读之星”,请你估计该校![]() 名学生中评为“阅读之星”的有多少人?
名学生中评为“阅读之星”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
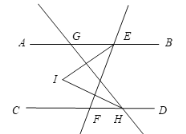
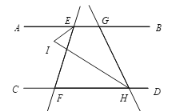
【题目】如图1,直线AB∥CD,直线EF交AB于点E,交CD于点F,点G和点H分别是直线AB和CD上的动点,作直线GH,EI平分∠AEF,HI平分∠CHG,EI与HI交于点I.
(1)如图,点G在点E的左侧,点H在点F的右侧,若∠AEF=70°,∠CHG=60°,求∠ETH的度数.
(2)如图,点G在点E的右侧,点H也在点F的右侧,若∠AEF=![]() ,∠CHG=β,其他条件不变,求∠ETH的度数.
,∠CHG=β,其他条件不变,求∠ETH的度数.
(3)如图,点G在点E的右侧,点H也在点F的右侧,∠GHC的平分线HJ交∠KEG的平分线EJ于点J.其他条件不变,若∠AEF=![]() ,∠CHG=β,求∠EJH的度数.
,∠CHG=β,求∠EJH的度数.
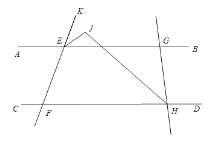
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商店要出售一种商品,出售时要在进价的基础上加上一定的利润,其销售量![]() (千克)与售价
(千克)与售价![]() (元)之间的关系如下表.
(元)之间的关系如下表.
销量 | 售价 |
1 | 1+0.3+0.05 |
2 | 2+0.6+0.05 |
3 | 3+0.9+0.05 |
4 | 4+1.2+0.05 |
... | ... |
(1)写出用含![]() 的式子表示售价
的式子表示售价![]() 的计算公式。
的计算公式。
(2)此商品的销售量为10千克时,售价为多少?
(3)当售价为26.05元时,商品的销售量为多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
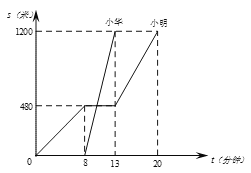
【题目】小明和小华是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校.如图是他们从家到学校已走的路程s(米)和所用时间t(分钟)的关系图.则下列说法中
①小明家与学校的距离1200米;
②小华乘坐公共汽车的速度是240米/分;
③小华乘坐公共汽车后7:50与小明相遇;
④小华的出发时间不变,当小华由乘公共汽车变为跑步,且跑步的速度是100米/分时,他们可以同时到达学校.其中正确的个数是( )
A. 1 个B. 2个
C. 3 个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个数表有7行7列,设aij表示第i行第j列上的数(其中i=1, 2, 3, ...7,j=1, 2, 3, …,7)

例如:第5行第3列上的数a53=7.
则: (1) (a23 -a22)+(a52 –a53)= _________.
(2)此数表中的四个数anp,ank, amp,amk.满足(anp -ank)+(amk -amp)=_ _________.
查看答案和解析>>
科目:初中数学 来源: 题型:
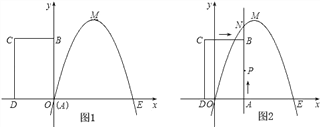
【题目】如图,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为(2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)求该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速度从如图所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).
①当t=![]() 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;
②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明同学将五个正方形按图1所示位置摆放后发现中间空白处是边长为3的小正方形,根据这个信息,小明设右下角的最小的正方形边长为x:
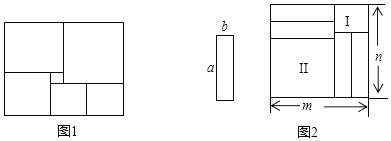
(1)则右上角最大的正方形边长为 ;
(2)求拼成的大长方形的长和宽分别为多少?
(3)小明又将四个长为a,宽为b的小长方形放到图2中的长方形中,得到如图2所示的图形,则图形Ⅰ和图形Ⅱ的周长之和是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com