
ЁОЬтФПЁПФГЙЋЫОЪдЯњвЛжжГЩБОЕЅМлЮЊ50дЊ/МўЕФаТВњЦЗЃЌЙцЖЈЪдЯњЪБЯњЪлЕЅМлВЛЕЭгкГЩБОЕЅМлЃЌгжВЛИпгк80дЊ/МўЃЌОЪдЯњЕїВщЃЌЗЂЯжЯњЪлСПyЃЈМўЃЉгыЯњЪлЕЅМлxЃЈдЊ/МўЃЉПЩНќЫЦПДзївЛДЮКЏЪ§yЃНkx+bЕФЙиЯЕЃЈШчЭМЫљЪОЃЉ
ЃЈIЃЉИљОнЭМЯѓЃЌЧѓвЛДЮКЏЪ§yЃНkx+bЕФНтЮіЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈЂђЃЉИУЙЋЫОвЊЯыУПЬьЛёЕУзюДѓЕФРћШѓЃЌгІАбЯњЪлЕЅМлЖЈЮЊЖрЩйЃПзюДѓРћШѓжЕЮЊЖрЩйЃП

ЁОД№АИЁПЃЈ1ЃЉy=Љx+100ЃЈ50ЁмxЁм80ЃЉЃЛЃЈ2ЃЉЯњЪлЕЅМлЖЈЮЊ75дЊ/МўЃЌзюДѓРћШѓЮЊ625дЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓвЛДЮКЏЪ§ЕФНтЮіЪНМДПЩЃЛЃЈ2ЃЉЩшУПЬьЛёЕУЕФРћШѓЮЊWдЊЃЌЙЙНЈРћШѓWгыЯњЪлЕЅМлxЕФЖўДЮКЏЪ§ФЃаЭЃЌИљОнЖўДЮКЏЪ§ЕФаджЪМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉгЩКЏЪ§ЕФЭМЯѓЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрЫљвдy=Љx+100ЃЈ50ЁмxЁм80ЃЉЃЛ
ЃЈ2ЃЉЩшУПЬьЛёЕУЕФРћШѓЮЊWдЊЃЌ
гЩЃЈ1ЃЉЕУЃКW=ЃЈxЉ50ЃЉy=ЃЈxЉ50ЃЉЃЈЉx+100ЃЉ=Љx2+150xЉ5000=ЉЃЈxЉ75ЃЉ2+625ЃЌ
ЁпЉ1ЃМ0ЃЌ
ЁрЕБx=75ЪБЃЌWзюДѓ=625МДИУЙЋЫОвЊЯыЕкЬьЛёЕУзюДѓРћШѓЃЌгІАбЯњЪлЕЅМлЮЊ75дЊ/МўЃЌзюДѓРћШѓЮЊ625дЊЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌAB=3ЃЌЕуEдкБпCDЩЯЃЌЧвCD=3DEЃЎНЋЁїADEбиAEЖделжСЁїAFEЃЌбгГЄEFНЛБпBCгкЕуGЃЌСЌНгAGЃЌCFЃЎЯТСаНсТлЃКЂйЕуGЪЧBCжаЕуЃЛЂкFG=FCЃЛЂл![]() ЃЎ
ЃЎ
Цфжае§ШЗЕФЪЧ

A. ЂйЂк B. ЂйЂл C. ЂкЂл D. ЂйЂкЂл
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭЌЪБХзжРСНУЖВФжЪОљдШЕФе§ЗНЬхїЛзгЃЌ
ЃЈ1ЃЉЭЈЙ§ЛЪїзДЭМЛђСаБэЃЌСаОйГіЫљгаЯђЩЯЕуЪ§жЎКЭЕФЕШПЩФмНсЙћЃЛ
ЃЈ2ЃЉЧѓЯђЩЯЕуЪ§жЎКЭЮЊ8ЕФИХТЪ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЧѓЯђЩЯЕуЪ§жЎКЭВЛГЌЙ§5ЕФИХТЪ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
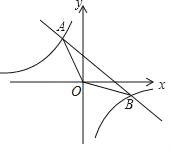
ЁОЬтФПЁПШчЭМЃЌOЮЊзјБъдЕуЃЌЕуAЃЈЉ1ЃЌ5ЃЉКЭЕуBЃЈmЃЌЉ1ЃЉОљдкЗДБШР§КЏЪ§![]() ЭМЯѓЩЯ
ЭМЯѓЩЯ
ЃЈ1ЃЉЧѓmЃЌkЕФжЕЃЛ
ЃЈ2ЃЉЕБxТњзуЪВУДЬѕМўЪБЃЌЉx+4ЃОЉ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉPЮЊyжсЩЯвЛЕуЃЌШєЁїABPЕФУцЛ§ЪЧЁїABOУцЛ§ЕФ2БЖЃЌжБНгаДГіЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌНЋ
ЃЌНЋ![]() ШЦЕу
ШЦЕу![]() а§зЊЃЌБп
а§зЊЃЌБп![]() ЗжБ№НЛБп
ЗжБ№НЛБп![]() ЁЂ
ЁЂ![]() гк
гк![]() ЁЂ
ЁЂ![]() СНЕу.
СНЕу.

ЃЈ1ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюаЁжЕЃЛ
ЕФзюаЁжЕЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЩш![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ЃЌЕБ
ЃЌЕБ![]() а§зЊЕН
а§зЊЕН![]() гы
гы![]() ЕФНЛЕу
ЕФНЛЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЪБЃЌЙ§Еу
ЕФжаЕуЪБЃЌЙ§Еу![]() зї
зї![]() ЕФДЙЯпНЛCMгкЕу
ЕФДЙЯпНЛCMгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
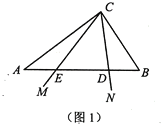
ЁОЬтФПЁПдкЫФБпаЮABCDжаЃЌЕуEЮЊABБпЩЯЕФвЛЕуЃЌЕуFЮЊЖдНЧЯпBDЩЯЕФвЛЕуЃЌЧвEFЁЭAB.
(1)ШєЫФБпаЮABCDЮЊе§ЗНаЮЃЎ
ЂйШчЭМЂйЃЌЧыжБНгаДГіAEгыDFЕФЪ§СПЙиЯЕ______________ЃЛ
ЂкНЋЁїEBFШЦЕуBФцЪБеыа§зЊЕНЭМЂкЫљЪОЕФЮЛжУЃЌСЌНгAEЃЌDFЃЌВТЯыAEгыDFЕФЪ§СПЙиЯЕВЂЫЕУїРэгЩЃЛ
(2)ШчЭМЂлЃЌШєЫФБпаЮABCDЮЊОиаЮЃЌBCЃНmABЃЌЦфЫћЬѕМўЖМВЛБфЃЌНЋЁїEBFШЦЕуBФцЪБеыа§зЊІС(0ЁуЃМІСЃМ90Ёу)ЕУЕНЁїEЁфBFЁфЃЌСЌНгAEЁфЃЌDFЁфЃЌЧыдкЭМЂлжаЛГіВнЭМЃЌВЂЧѓГіAEЁфгыDFЁфЕФЪ§СПЙиЯЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
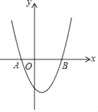
ЁОЬтФПЁПШчЭМЃЌPЪЧХзЮяЯпyЃНx2Љ4x+3ЩЯЕФвЛЕуЃЌвдЕуPЮЊдВаФЁЂ1ИіЕЅЮЛГЄЖШЮЊАыОЖзїЁбPЃЌЕБЁбPгыжБЯпyЃН0ЯрЧаЪБЃЌЕуPЕФзјБъЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаХзЮяЯпyЃНЃЈx+1ЃЉЃЈxЉ3ЃЉгыxжсЯрНЛгкAЁЂBСНЕуЃЌШєдкХзЮяЯпЩЯгаЧвжЛгаШ§ИіВЛЭЌЕФЕуC1ЁЂC2ЁЂC3ЃЌЪЙЕУЁїABC1ЁЂЁїABC2ЁЂЁїABC3ЕФУцЛ§ЖМЕШгкmЃЌдђmЕФжЕЪЧЃЈЁЁЁЁЃЉ
A. 6 B. 8 C. 12 D. 16
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШЅбЇаЃЪГЬУОЭВЭЃЌОГЃЛсдквЛИіТђВЫДАПкЧАЕШД§ЃЌОЕїВщЗЂЯжЃЌЭЌбЇЕФЪцЪЪЖШжИЪ§yгыЕШЪБМфxЃЈЗжЃЉжЎМфТњзуЗДБШР§КЏЪ§ЙиЯЕЃЌШчЯТБэЃК
ЕШД§ЪБМфx | 1 | 2 | 5 | 10 | 20 |
ЪцЪЪЖШжИЪ§y | 100 | 50 | 20 | 10 | 5 |
вбжЊбЇЩњЕШД§ЪБМфВЛГЌЙ§30Зжжг
ЃЈ1ЃЉЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉШєЕШД§ЪБМф8ЗжжгЪБЃЌЧѓЪцЪЪЖШЕФжЕЃЛ
ЃЈ3ЃЉЪцЪЪЖШжИЪ§ВЛЕЭгк10ЪБЃЌЭЌбЇВХЛсИаЕНЪцЪЪЃЎЧыЫЕУїЃЌзїЮЊЪГЬУЕФЙмРэдБЃЌШУУПИідкДАПкТђВЫЕФЭЌбЇзюЖрЕШД§ЖрЩйЪБМфЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com