
【题目】在四边形ABCD中,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.
(1)若四边形ABCD为正方形.
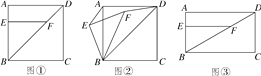
①如图①,请直接写出AE与DF的数量关系______________;
②将△EBF绕点B逆时针旋转到图②所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由;
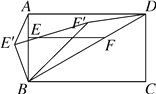
(2)如图③,若四边形ABCD为矩形,BC=mAB,其他条件都不变,将△EBF绕点B逆时针旋转α(0°<α<90°)得到△E′BF′,连接AE′,DF′,请在图③中画出草图,并求出AE′与DF′的数量关系.
【答案】(1)①DF=![]() AE
AE
②DF=![]() AE.理由见解析; (2) DF′=
AE.理由见解析; (2) DF′=![]() AE′.
AE′.
【解析】试题分析:
(1)①由四边形ABCD是正方形易得BD=![]() AB,由EF∥AD可得
AB,由EF∥AD可得![]() ,从而可DF=
,从而可DF=![]() AE;
AE;
②由旋转的性质结合题意可证△ABE∽△DBF可得![]() ,从而可得DF=
,从而可得DF=![]() AE;
AE;
(2)画图如下,由四边形ABCD为矩形,可得AD=BC=mAB,由勾股定理可得BD=![]() =
=![]() AB;易证△BEF∽△BAD,可得
AB;易证△BEF∽△BAD,可得![]() ,因此
,因此![]() =
=![]() .
.
由旋转性质结合题意可证△ABE′∽△DBF′,由此可得![]() =
=![]() =
=![]() ,
,
∴DF′=![]() AE′.
AE′.
试题解析:
(1)①DF=![]() AE
AE
②DF=![]() AE.理由如下:
AE.理由如下:
∵△EBF绕点B逆时针旋转到图②所示的位置,
∴∠ABE=∠DBF.
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴△ABE∽△DBF,
∴![]() ,即DF=
,即DF=![]() AE.
AE.
(2)如图所示,∵四边形ABCD为矩形,
∴AD=BC=mAB,
∴BD=![]() =
=![]() AB.
AB.
∵EF⊥AB,
∴EF∥AD,
∴△BEF∽△BAD,
∴![]() ,
,
∴![]() =
=![]() .
.
∵△EBF绕点B逆时针旋转α(0°<α<90°)得到△E′BF′,
∴∠ABE′=∠DBF′,BE′=BE,BF′=BF,
∴![]() =
=![]() =
=![]() ,
,
∴△ABE′∽△DBF′,
∴![]() =
=![]() =
=![]() ,即DF′=
,即DF′=![]() AE′.
AE′.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
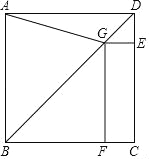
【题目】如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明坐于堤边垂钓,如图①,河堤AC的坡角为30°,AC长![]() 米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离(如图②).
米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离(如图②).
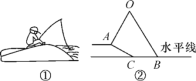
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区某校为了加强对学生的安全教育工作,开展了安全知识竞赛,该校在初三年级中随机抽取了一部分同学的竞赛成绩,并把抽取的竞赛成绩分成优、良、中、差四个等级,同时绘制了如下两幅不完整的统计图,请根据统计图提供的信息解答以下问题:
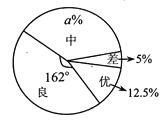
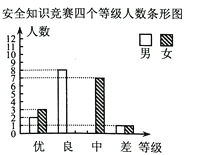
(1)该校在初三年级中随机抽取了多少名同学的竞赛成绩?
(2)求扇形统计图中![]() 的值,并补全条形统计图;
的值,并补全条形统计图;
(3)若从优等中选出两名同学在全年级进行交流,请用列表或树状图的方法求出所选两名学生恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示)
(I)根据图象,求一次函数y=kx+b的解析式,并写出自变量x的取值范围;
(Ⅱ)该公司要想每天获得最大的利润,应把销售单价定为多少?最大利润值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
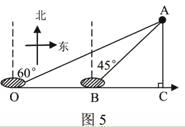
【题目】如图5,在A岛周围25海里水域有暗礁,一轮船由西向东航行到O处时,发现A岛在北偏东60°方向,轮船继续前行20海里到达B处发现A岛在北偏东45°方向,该船若不改变航向继续前进,有无触礁的危险? (参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形纸片ABCD的边长为8,⊙O的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA′恰好与⊙O相切于点A′(△EFA′与⊙O除切点外无重叠部分),延长FA′交CD边于点G,则A′G的长是( )
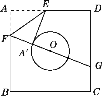
A. 6 B. ![]() C. 7 D.
C. 7 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.解答以下问题
(1)小球从飞出到落地要用多少时间?
(2)小球飞行的最大高度是多少?此时需要多少飞行时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
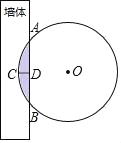
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在墙壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”问题题意为:如图,有一圆柱形木材埋在墙壁中,不知其直径大小.用锯去锯这木材,锯口深1寸(即CD=1寸),锯道长1尺(即AB=1尺),问这圆形木材直径是多少?(注:1尺=10寸)由此,可求出这圆形木材直径为______寸.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com