
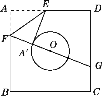
【题目】如图,已知正方形纸片ABCD的边长为8,⊙O的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA′恰好与⊙O相切于点A′(△EFA′与⊙O除切点外无重叠部分),延长FA′交CD边于点G,则A′G的长是( )
A. 6 B. ![]() C. 7 D.
C. 7 D. ![]()
【答案】B
【解析】
连AC,过F作FH⊥CD于H. 由题干条件易证明点F、A'、O共线,即FG过圆心O,再由∠A=∠COG、∠AOF=∠COG可证明△COG≌AOF,得AF=CG、OF=OG;设FA=x,将FG和HG用含x式子表示,在RT△FGH中运用勾股定理即可求解.
解:
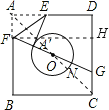
由题干条件可知FA=FA’,∠A=∠EA’F,再由EA′恰好与⊙O相切于点A′可得OA’⊥EA’,则点F、A'、O共线,即FG过圆心O,则OA=OC;
再由∠A=∠COG、∠AOF=∠COG可证明△COG≌AOF,则AF=CG、OF=OG,再由OA’=ON可得FA’=GN;
设FA=x,则FA=FA’=DH=CG=GN=x,FG=GA’+A’N+NG=2x+4,HG=DC-DH-CG=8-2x,
在RT△FGH中,FG2=FH2+HG2,则(2x+4)2=82+(8-2x)2,解得x=![]() ,
,
则A’G=A’N+NG=4+![]() =
=![]() ,
,
故选择B.


科目:初中数学 来源: 题型:
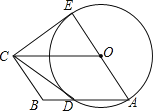
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=3,CD=4,求平行四边形OABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
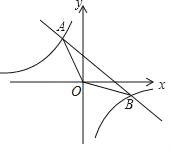
【题目】如图,O为坐标原点,点A(﹣1,5)和点B(m,﹣1)均在反比例函数![]() 图象上
图象上
(1)求m,k的值;
(2)当x满足什么条件时,﹣x+4>﹣![]() ;
;
(3)P为y轴上一点,若△ABP的面积是△ABO面积的2倍,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
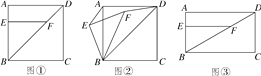
【题目】在四边形ABCD中,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.
(1)若四边形ABCD为正方形.
①如图①,请直接写出AE与DF的数量关系______________;
②将△EBF绕点B逆时针旋转到图②所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由;
(2)如图③,若四边形ABCD为矩形,BC=mAB,其他条件都不变,将△EBF绕点B逆时针旋转α(0°<α<90°)得到△E′BF′,连接AE′,DF′,请在图③中画出草图,并求出AE′与DF′的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
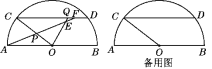
【题目】已知:如图,AB是半圆O的直径,弦CD∥AB,动点P、Q分别在线段OC、CD上,且DQ=OP,AP的延长线与射线OQ相交于点E、与弦CD相交于点F(点F与点C、D不重合),AB=20,cos ∠AOC=![]() .设OP=x,△CPF的面积为y.
.设OP=x,△CPF的面积为y.
(1)求证:AP=OQ;
(2)求y关于x的函数关系式,并写出x的取值范围;
(3)当△OPE是直角三角形时,求线段OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中抛物线y=(x+1)(x﹣3)与x轴相交于A、B两点,若在抛物线上有且只有三个不同的点C1、C2、C3,使得△ABC1、△ABC2、△ABC3的面积都等于m,则m的值是( )
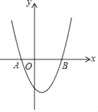
A. 6 B. 8 C. 12 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
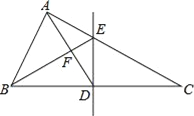
【题目】如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
(1)判断△FDB与△ABC是否相似,并说明理由.
(2)AF与DF相等吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
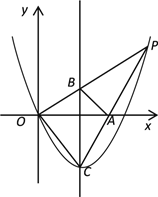
【题目】如图,已知抛物线y=ax2+bx的顶点为C(1,![]() ),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
(1)求该抛物线的表达式;
(2)如果点P的横坐标为m,试用m的代数式表示线段BC的长;
(3)如果△ABP的面积等于△ABC的面积,求点P坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com