
����Ŀ����֪����ͼ��AB�ǰ�ԲO��ֱ������CD��AB������P��Q�ֱ����߶�OC��CD�ϣ���DQ��OP��AP���ӳ���������OQ�ཻ�ڵ�E������CD�ཻ�ڵ�F(��F���C��D���غ�)��AB��20��cos ��AOC��![]() .��OP��x����CPF�����Ϊy.
.��OP��x����CPF�����Ϊy.
(1)��֤��AP��OQ��
(2)��y����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
(3)����OPE��ֱ��������ʱ�����߶�OP�ij���
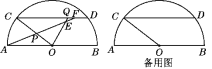
���𰸡���1�������������2��y��![]() ��x��ȡֵ��ΧΪ
��x��ȡֵ��ΧΪ![]() <x<10����3���߶�OP�ij�Ϊ8.
<x<10����3���߶�OP�ij�Ϊ8.
��������
��1������OD��������ֱ��ƽ�У��ڴ�����Ⱥ͵ȱ߶ԵȽǵ����ʿɵó���AOC����ODC�������ñ߽DZߵ��ж϶�����֤����AOP�ա�ODQ������ȫ�������ζ�Ӧ����ȼ���֤��AP��OQ.
��2������P��PH��OA�ڵ�H������O��OG��CD�ڵ�G.������ֱ��ƽ�У��ڴ�����ȿ�֤����PFC�ס�PAO���������Ǻ����ļ��㹫ʽ���ɶ�������x��ʾ����PAO��������������������������֮�ȵ������Ʊȵ�ƽ��������x��ʾ��y���ֱ�ȡ��F���D�͵�C�غ�ʱ�����ô������������������ε����ʿ����x��ֵ����Ϊ��F���C��D���غϣ����ɵó�X��ȡֵ��Χ��
��3�����������֪������POEΪֱ��������ʱ���ɷ�����������ۣ�����POE=90�㡢��OPE=90�㡢��OEP=90�����ֱ������������OP�ij�����ȡ���ϣ�2����x��ȡֵ��Χ�Ľ����
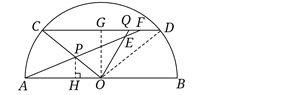
(1)֤��������OD��
��OC��OD��
���OCD����ODC.
��CD��AB�����AOC����OCD��
���AOC����ODC.
����AOP����ODQ��
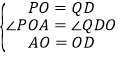
���AOP�ա�ODQ��
��AP��OQ.
(2)��PH��OA������ΪH����OG��CD������ΪG.
��cos��AOC=![]() �ɵ�OH��
�ɵ�OH��![]() x��
x��
��RT��OPH�У��ɹ��ɶ����ɵã�PH=![]() ��
��
��S��AOP��![]() =3x.
=3x.
��CD��AB��
���PFC�ס�PAO��
��![]() ��
��
��![]() =
=![]() .
.
����F���C�غ�ʱ��OP��10.
����F���D�غ�ʱ��
��cos��OCG��![]() ��cos��AOC��
��cos��AOC��![]() ��
��
��CG��8��
��CD��16.
��![]() ��
��
��![]()
���x��![]() .
.
������F���C��D���غϣ�
��x��ȡֵ��ΧΪ![]() <x<10.
<x<10.
(3)�⣺����POE��90��ʱ��CQ��![]() ��OP��DQ��CD��CQ��3.5(��ȥ)��
��OP��DQ��CD��CQ��3.5(��ȥ)��
����OPE��90��ʱ������APO��90�㣬
��OP��AO��cos��COA��8��
����OEP��90��ʱ��������������ڣ�
���߶�OP�ij�Ϊ8.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
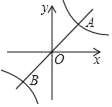
����Ŀ����ͼ��һ�κ���y��x��ͼ���뷴��������y�T![]() ��ͼ����A��B���㣬�ҵ�A����Ϊ��1��m����
��ͼ����A��B���㣬�ҵ�A����Ϊ��1��m����
��1����˷����������Ľ���ʽ��
��2����xȡ��ֵʱ��һ�κ������ڷ�����������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ijУΪ�˼�ǿ��ѧ���İ�ȫ������������չ�˰�ȫ֪ʶ��������У�ڳ����꼶�������ȡ��һ����ͬѧ�ľ����ɼ������ѳ�ȡ�ľ����ɼ��ֳ��š������С����ĸ��ȼ���ͬʱ����������������������ͳ��ͼ�������ͳ��ͼ�ṩ����Ϣ����������⣺
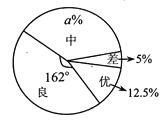
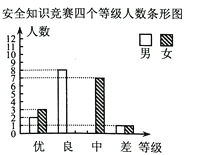
��1����У�ڳ����꼶�������ȡ�˶�����ͬѧ�ľ����ɼ���
��2��������ͳ��ͼ��![]() ��ֵ������ȫ����ͳ��ͼ��
��ֵ������ȫ����ͳ��ͼ��
��3�������ŵ���ѡ������ͬѧ��ȫ�꼶���н����������б�����״ͼ�ķ��������ѡ����ѧ��ǡ����һ��һŮ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
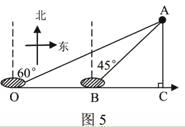
����Ŀ����ͼ5����A����Χ25����ˮ���а�����һ�ִ��������е�O��ʱ������A���ڱ�ƫ��60�������ִ�����ǰ��20���ﵽ��B������A���ڱ�ƫ��45�����ô������ı亽�����ǰ������������Σ�գ� ���ο����ݣ�![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ֽƬABCD�ı߳�Ϊ8����O�İ뾶Ϊ2��Բ���������ε������ϣ���ֽƬ��ͼʾ��ʽ�۵���ʹEA��ǡ������O�����ڵ�A��(��EFA������O���е������ص�����)���ӳ�FA����CD���ڵ�G����A��G�ij���(����)
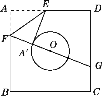
A. 6 B. ![]() C. 7 D.
C. 7 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ű�����ȫ��ͬ��ֽ��A��B��C����������ֱ������ֲ�ͬ�ļ���ͼ�Σ�С������3��ֽ�Ʊ��泯��ϴ�Ⱥ�����һ�ţ��Ż�ϴ�Ⱥ�������һ�ţ������û���״ͼ���б��ķ�����������������ֽ��������������ͼ�μ�����Գ�ͼ���������ĶԳ�ͼ�εĸ��ʣ�
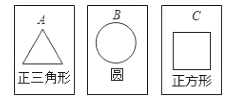
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����40m/s���ٶȽ�С����������30���ǵķ������ʱ��С��ķ���·�߽���һ�������ߣ���������ǿ���������С��ķ��и߶�h����λ��m�������ʱ��t����λ��s��֮����к�����ϵh��20t��5t2�������������
��1��С��ӷɳ������Ҫ�ö���ʱ�䣿
��2��С����е����߶��Ƕ��٣���ʱ��Ҫ���ٷ���ʱ�䣿

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ֽ��,ÿ��ֽ���ڸ�װ��4�����ʡ���С����ͬ��ƹ����,����һ��ֽ����4��С���Ϸֱ�д��1��2��3��4��4��������һ��ֽ����4��С���Ϸֱ�д��5��6��7��8��4�������ס��������̶���һ����Ϸ�������ǣ���������ֽ���и��������һ��С��Ȼ�������С���ϵ�������ˣ����õ��Ļ���2�ı��������1�֣����õ�����3�ı��������ҵ�2��.���һ����Ϸ��,����ֱ�Żظ��Ե�ֽ��,ҡ�Ⱥ������һ����Ϸ,���÷ָ���ʤ��.��
(1)����ͨ���б�(����״ͼ)�ֱ����˻���2�ı�����3�ı����ĸ���;
(2)����Ϊ�����Ϸ��ƽ��?Ϊʲô?������Ϊ����ƽ,�����ĵ÷ֹ���,ʹ��Ϸ��˫����ƽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ����������ҹ���������ѧ�����������������е�һ�����⣬������Բ�ģ����ڱ��У���֪��С���Ծ��֮����һ�磬�����һ�ߣ��ʾ����Σ��� ���ִ�����ѧ���Ա����ǣ�����ͼ��CD�ǡ�O��ֱ������AB��CD������ΪE��CE = 1�磬AB = 1�ߣ���ֱ���ij���. �����⣬CD��Ϊ�� ��
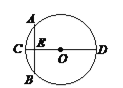
A. ![]() �� B. 13�� C. 25�� D. 26��
�� B. 13�� C. 25�� D. 26��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com