
【题目】如图矩形COAB,点B(4,3),点H位于边BC上.

直线l1:2x﹣y+3=0
直线l2:2x﹣y﹣3=0
(1)若点N为l2上第一象限的点,△AHN为等腰Rt△,求N坐标.
(2)若把l1、l2上的点构成的图形称为图形V.已知矩形AJHI的顶点J在图形V上,I为平面系上的点,且J(x,y),求x的范围(写出过程).
【答案】(1)点N的坐标为(![]() ,
,![]() );(2,1);(
);(2,1);(![]() ,
,![]() );(2)x的取值范围为﹣
);(2)x的取值范围为﹣![]() ≤x<0或0<x≤
≤x<0或0<x≤![]() 或
或![]() ≤x≤2或
≤x≤2或![]() ≤x≤
≤x≤![]() .
.
【解析】
(1)分点A、H、N分别为直角时的三种情况,根据等腰直角三角形的性质,设点N的坐标利用全等三角形的关系求出x的值即可得到答案;
(2)当点J在l2上,分两种情况:点H与点B重合时与点C重合时,利用直角三角形斜边中线等于斜边的一半及勾股定理求出点J的坐标,即可得到取值范围,同样的方法求出点J在l1上时x的取值范围即可得到答案.
(1)①若点A为直角顶点时,点N在第一象限,连结AC,
如图1,∠AHB>∠ACB>45°,
∴△AHN不可能是等腰直角三角形,
∴点N不存在;
②若点H为直角顶点时,点N在第一象限,如图1,
过点N作MN⊥CB,交CB的延长线于点M,
则Rt△ABH≌Rt△HMN,
∴AB=HM=4,MN=HB,
设N(x,2x﹣3),则MN=x﹣4,
∴2x﹣3=4+3﹣(x﹣4),
x=![]() ,
,
∴N(![]() ,
,![]() );
);
③若点N为直角顶点时,点N在第一象限,如图2,
设N1(x,2x﹣3),
过点N1作N1G1⊥OA,交BC于点P1,
则Rt△AN1G1≌Rt△HM1P1,
∴AG1=N1P1=3﹣(2x﹣3),
∴x+3﹣(2x﹣3)=4,
x=2,
∴N1(2,1);
设N2(x,2x﹣3),
同理可得x+2x﹣3﹣3=4,
∴x=![]() ,
,
∴N2(![]() ,
,![]() );
);
综上所述,点N的坐标为(![]() ,
,![]() );(2,1);(
);(2,1);(![]() ,
,![]() );
);
(2)当点J在直线l2上时,
∵点J的横坐标为x,
∴J(x,2x﹣3),
当点H和点B重合时,H(4,3),
∴AH的中点G坐标为(2,3),
∵四边形AJHI是矩形,
∴∠AJB=90°,
∴JG=![]() AH=2,
AH=2,
∴(x﹣2)2+(2x﹣3﹣3)2=4,
∴x=![]() (点J在AB上方的横坐标)或x=2(点J在AB下方的横坐标),
(点J在AB上方的横坐标)或x=2(点J在AB下方的横坐标),
当点H和点C重合时,H(4,0),AH的中点G'坐标为(2,![]() ),
),
同理:JG'=![]() AH=
AH=![]() ,
,
∴(x﹣2)2+(2x﹣3﹣![]() )2=
)2=![]() ,
,
∴x=![]() (和点J在AB上方构成的四边形是矩形的横坐标)或x=
(和点J在AB上方构成的四边形是矩形的横坐标)或x=![]() (和点J在AB下方构成的四边形是矩形的横坐标)
(和点J在AB下方构成的四边形是矩形的横坐标)
∴![]() ≤x≤
≤x≤![]() 或
或![]() ≤x≤2.
≤x≤2.
当点J在l1上时,同理:﹣![]() ≤x<0或0<x≤
≤x<0或0<x≤![]() .
.
综上所述,x的取值范围为﹣![]() ≤x<0或0<x≤
≤x<0或0<x≤![]() 或
或![]() ≤x≤2或
≤x≤2或![]() ≤x≤
≤x≤![]() .
.




 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
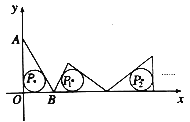
【题目】如图,在![]() 置于平面直角坐标系中,点
置于平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 内切圆的圆心.将
内切圆的圆心.将![]() 沿
沿![]() 轴的正方向作无滑动滚动,使它的三边依次与
轴的正方向作无滑动滚动,使它的三边依次与![]() 轴重合,第一次滚动后圆心为
轴重合,第一次滚动后圆心为![]() ,第二次滚动后圆心为
,第二次滚动后圆心为![]() ,…,依此规律,第2020次滚动后,
,…,依此规律,第2020次滚动后,![]() 内切圆的圆心
内切圆的圆心![]() 的坐标是__________.
的坐标是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
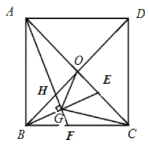
【题目】如图,在正方形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 为
为![]() 上动点(不与
上动点(不与![]() 、
、![]() 重合),作
重合),作![]() ,垂足为
,垂足为![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() 、
、![]() ,连接
,连接![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC的纸片中,∠C=90°,AC=5,AB=13.点D在边BC上,以AD为折痕将△ADB折叠得到△ADB′,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
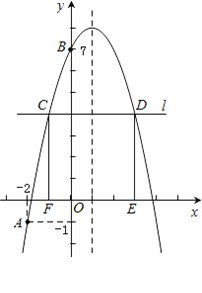
【题目】如图,已知二次函数y=-x2+bx+c的图象经过A(-2,-1),B(0,7)两点.
(1)求该抛物线的解析式及对称轴;
(2)当x为何值时,y>0?
(3)在x轴上方作平行于x轴的直线l,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作x轴的垂线,垂足分别为F,E.当矩形CDEF为正方形时,求C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
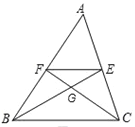
【题目】如图,在△ABC中,中线BE、CF相交于点G,连接EF,下列结论:
①![]() =
=![]() ; ②
; ②![]() =
=![]() ; ③
; ③![]() =
=![]() ; ④
; ④![]() =
=![]() .其中正确的个数有( )
.其中正确的个数有( )
A. 1个 B. C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
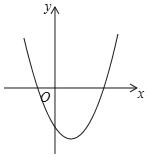
【题目】如图,在平直角坐标系中,O为坐标原点,抛物线y=x2﹣mx﹣1的对称轴为直线x=1.若关于x的一元二次方程x2﹣mx﹣1﹣n=0(n为实数)在0<x<3的范围内有解,则n的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
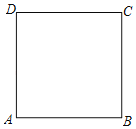
【题目】已知正方形ABCD的边长为10,现改变该正方形的边长,使其变为矩形.若AD的长增加了x,AB的长减少了kx(其中k>0,x>0).
(1)若k=2,请说明改变后得到的矩形面积是否可为125;
(2)若改变后得到的矩形面积仍为100,求x与k的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com