
【题目】如图,在Rt△ABC的纸片中,∠C=90°,AC=5,AB=13.点D在边BC上,以AD为折痕将△ADB折叠得到△ADB′,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是___.

【答案】7或![]() .
.
【解析】
由勾股定理可以求出BC的长,由折叠可知对应边相等,对应角相等,当△DEB′为直角三角形时,可以分为两种情况进行考虑,分别利用勾股定理可求出BD的长.
在Rt△ABC中,![]() ,
,
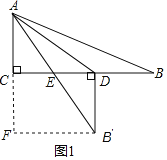
(1)当∠EDB′=90°时,如图1,
过点B′作B′F⊥AC,交AC的延长线于点F,
由折叠得:AB=AB′=13,BD=B′D=CF,
设BD=x,则B′D=CF=x,B′F=CD=12﹣x,
在Rt△AFB′中,由勾股定理得:
![]() ,
,
即:x2﹣7x=0,解得:x1=0(舍去),x2=7,
因此,BD=7.
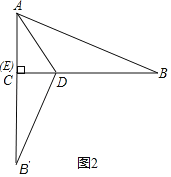
(2)当∠DEB′=90°时,如图2,此时点E与点C重合,
由折叠得:AB=AB′=13,则B′C=13﹣5=8,
设BD=x,则B′D=x,CD=12﹣x,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,解得:
,解得:![]() ,
,
因此![]() .
.
故答案为:7或![]() .
.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点B在x轴上,点A、点C在双曲线y=![]() (k>0,x>0)上.若直线BC的解析式为y=
(k>0,x>0)上.若直线BC的解析式为y=![]() x﹣2,则k的值为( )
x﹣2,则k的值为( )
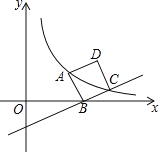
A.24B.12C.6D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D在AB的延长线上,C、E是⊙O上的两点,CE=CB,∠BCD=∠CAE,延长AE交BC的延长线于点F.
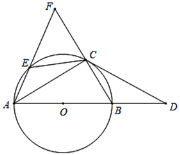
求证:(1)CD是⊙O的切线;
(2)CE=CF;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的差是( )

A.6B.2![]() +1C.9D.7
+1C.9D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图矩形COAB,点B(4,3),点H位于边BC上.

直线l1:2x﹣y+3=0
直线l2:2x﹣y﹣3=0
(1)若点N为l2上第一象限的点,△AHN为等腰Rt△,求N坐标.
(2)若把l1、l2上的点构成的图形称为图形V.已知矩形AJHI的顶点J在图形V上,I为平面系上的点,且J(x,y),求x的范围(写出过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
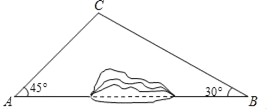
【题目】为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
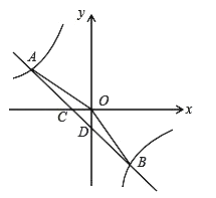
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第二、四象限内的
的图象交于第二、四象限内的![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() ,连接
,连接![]() ,且
,且![]() .
.
(1)求这个反比例函数和一次函数的解析式;
(2)根据图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用画树状图的方法画出的某个试验的所有可能发生的结果,则这个试验不可能是( )
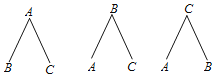
A.在一个不透明的袋中有3个除颜色外完全相同的小球,其中两个黑球,一个白球,从中随机取出两个球
B.小明,小王两个人在一个路口,分别从直行,左转,右转三个方向中随机选一个方向
C.从某学习小组的两名男生和一名女生中随机选取两名学生进行竞答
D.体育测试中,随机从足球运球,篮球运球,排球垫球三个项目中选择两个项目
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com