
����Ŀ��ij������Ҫ�ڹ涨ʱ���ڰ���1200�ֻ���ԭ�ϣ�����![]() ��
��![]() ���ֻ����˿ɹ�ѡ����֪
���ֻ����˿ɹ�ѡ����֪![]() �ͻ����˱�
�ͻ����˱�![]() �ͻ�����ÿСʱ�����30���ͣ�
�ͻ�����ÿСʱ�����30���ͣ�![]() �����˰���900�����õ�ʱ����
�����˰���900�����õ�ʱ����![]() �ͻ����˰���600�����õ�ʱ����ȣ�
�ͻ����˰���600�����õ�ʱ����ȣ�
(1)�����ֻ�����ÿСʱ�ֱ���˶��ٶֻ���ԭ�ϣ�
(2)�ù���ԭ�ƻ�ͬʱʹ�������ֻ����˰��ˣ�����һ��ʱ���![]() �ͻ������������µİ����������뿪�������뱣֤��������ԭ����11Сʱ��ȫ��������ϣ���
�ͻ������������µİ����������뿪�������뱣֤��������ԭ����11Сʱ��ȫ��������ϣ���![]() �ͻ��������ٹ�������Сʱ�����ܱ�֤��������ԭ���ڹ涨��ʱ������ɣ�
�ͻ��������ٹ�������Сʱ�����ܱ�֤��������ԭ���ڹ涨��ʱ������ɣ�
���𰸡���1��![]() �ͻ�����ÿСʱ����90�ֻ���ԭ�ϣ�
�ͻ�����ÿСʱ����90�ֻ���ԭ�ϣ�![]() �ͻ�����ÿСʱ����60�ֻ���ԭ�ϣ���2��A�ͻ��������ٹ���6Сʱ�����ܱ�֤��������ԭ���ڹ涨��ʱ������ɣ�
�ͻ�����ÿСʱ����60�ֻ���ԭ�ϣ���2��A�ͻ��������ٹ���6Сʱ�����ܱ�֤��������ԭ���ڹ涨��ʱ������ɣ�
��������
(1) ��B�ͻ�����ÿСʱ����x�ֻ���ԭ�ϣ���A�ͻ�����ÿСʱ����(x+30)�ֻ���ԭ�ϣ�����A�ͻ����˰���900�����õ�ʱ����B�ͻ����˰���600�����õ�ʱ����Ƚ�������������Ϳ��Եó�����.
(2) ��A�ͻ����˹���tСʱ��������������ԭ����11Сʱ��ȫ����������г�����ʽ��⣮
�⣺��1����![]() �ͻ�����ÿСʱ����
�ͻ�����ÿСʱ����![]() �ֻ���ԭ�ϣ���
�ֻ���ԭ�ϣ���![]() �ͻ�����ÿСʱ����
�ͻ�����ÿСʱ����![]() �ֻ���ԭ�ϣ�
�ֻ���ԭ�ϣ�
�������⣬��
![]() �����
�����![]() ��
��
�����飬![]() �����з��̵Ľ⣮
�����з��̵Ľ⣮
��![]() ʱ��
ʱ��![]() ��
��
��![]() �ͻ�����ÿСʱ����90�ֻ���ԭ�ϣ�
�ͻ�����ÿСʱ����90�ֻ���ԭ�ϣ�![]() �ͻ�����ÿСʱ����60�ֻ���ԭ�ϣ�
�ͻ�����ÿСʱ����60�ֻ���ԭ�ϣ�
��2����![]() �ͻ����˹���
�ͻ����˹���![]() Сʱ��
Сʱ��
�������⣬��![]() �����
�����![]() ��
��
��: A�ͻ��������ٹ���6Сʱ�����ܱ�֤��������ԭ���ڹ涨��ʱ������ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
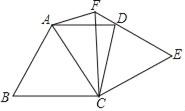
����Ŀ����ͼ�����ȱߡ�ABC�Ƶ�C˳ʱ����ת90��õ���EFC����ACE��ƽ����CD��EF�ڵ�D������AD��AF��
��1�����CFA������
��2����֤��AD��BC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
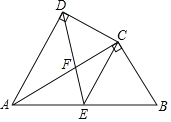
����Ŀ����ͼ���ı���ABCD�У�ACƽ�֡�BAD����ADC����ACB��90����EΪAB���е㣬AC��DE���ڵ�F��
��1����֤��CE��AD��
��2����֤��AC2��ABAD��
��3����AC��2![]() ��AB��4����
��AB��4����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��P��B��C�ǡ�O�ϵ��ĸ��㣬��DAP����PBA��
��1����֤��AD�ǡ�O�����ߣ�
��2������APC����BPC��60������̽���߶�PA��PB��PC֮���������ϵ����֤����Ľ��ۣ�
��3���ڵڣ�2���ʵ������£���AD��2��PD��1�����߶�AC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=8���ף�AC=16���ף���P��A��������ÿ��2�����ٶ���B�˶�����Q��Cͬʱ��������ÿ��3�����ٶ���A�˶�������һ�����㵽�˵�ʱ����һ������Ҳ��Ӧֹͣ�˶�����ô������A��P��QΪ���������������ABC����ʱ���˶�ʱ��Ϊ_________________
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ����ƽ��ֱ������ϵ�У���
����ƽ��ֱ������ϵ�У���![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��![]() ����Բ��Բ�ģ���
����Բ��Բ�ģ���![]() ��
��![]() ���������������������ʹ��������������
���������������������ʹ��������������![]() ���غϣ���һ�ι�����Բ��Ϊ
���غϣ���һ�ι�����Բ��Ϊ![]() ���ڶ��ι�����Բ��Ϊ
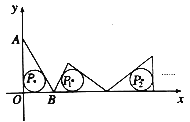
���ڶ��ι�����Բ��Ϊ![]() ���������˹��ɣ���2020�ι�����
���������˹��ɣ���2020�ι�����![]() ����Բ��Բ��
����Բ��Բ��![]() ��������__________��
��������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() �У��Խ���
�У��Խ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() Ϊ
Ϊ![]() �϶��㣨����
�϶��㣨����![]() ��
��![]() �غϣ�����
�غϣ�����![]() ������Ϊ
������Ϊ![]() ���ֱ�
���ֱ�![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() ��
��
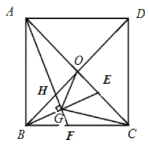
��1����֤��![]() ��
��
��2����![]() �Ķ�����
�Ķ�����
��3����![]() ��
��![]() ����
����![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
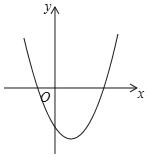
����Ŀ����ͼ����ƽֱ������ϵ�У�OΪ����ԭ�㣬������y=x2��mx��1�ĶԳ���Ϊֱ��x=1��������x��һԪ���η���x2��mx��1��n=0(nΪʵ��)��0��x��3�ķ�Χ���н⣬��n��ȡֵ��Χ��______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com