
【题目】如图,点A,P,B,C是⊙O上的四个点,∠DAP=∠PBA.
(1)求证:AD是⊙O的切线;
(2)若∠APC=∠BPC=60°,试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)在第(2)问的条件下,若AD=2,PD=1,求线段AC的长.

【答案】(1)证明见解析;(2)PA+PB=PF+FC=PC;(3)1+![]() .
.
【解析】
(1)欲证明AD是⊙O的切线,只需推知AD⊥AE即可;
(2)首先在线段PC上截取PF=PB,连接BF,进而得出△BPA≌△BFC(AAS),即可得出PA+PB=PF+FC=PC;
(3)利用△ADP∽△BDA,得出![]() =
=![]() =
=![]() ,求出BP的长,进而得出△ADP∽△CAP,则
,求出BP的长,进而得出△ADP∽△CAP,则![]() =
=![]() ,则AP2=CPPD求出AP的长,即可得出答案.
,则AP2=CPPD求出AP的长,即可得出答案.
(1)证明:先作⊙O的直径AE,连接PE,

∵AE是直径,
∴∠APE=90°.
∴∠E+∠PAE=90°.
又∵∠DAP=∠PBA,∠E=∠PBA,
∴∠DAP=E,
∴∠DAP+∠PAE=90°,即AD⊥AE,
∴AD是⊙O的切线;
(2)PA+PB=PC,
证明:在线段PC上截取PF=PB,连接BF,
∵PF=PB,∠BPC=60°,
∴△PBF是等边三角形,
∴PB=BF,∠BFP=60°,
∴∠BFC=180°﹣∠PFB=120°,
∵∠BPA=∠APC+∠BPC=120°,
∴∠BPA=∠BFC,
在△BPA和△BFC中,
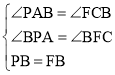 ,
,
∴△BPA≌△BFC(AAS),
∴PA=FC,AB=CB,
∴PA+PB=PF+FC=PC;
(3)∵△ADP∽△BDA,
∴![]() =
=![]() =
=![]() ,
,
∵AD=2,PD=1,
∴BD=4,AB=2AP,
∴BP=BD﹣DP=3,
∵∠APD=180°﹣∠BPA=60°,
∴∠APD=∠APC,
∵∠PAD=∠E,∠PCA=∠E,
∴∠PAD=∠PCA,
∴△ADP∽△CAP,
∴![]() =
=![]() ,
,
∴AP2=CPPD,
∴AP2=(3+AP)1,
解得:AP=![]() 或AP=
或AP=![]() (舍去),
(舍去),
由(2)知△ABC是等边三角形,
∴AC=BC=AB=2AP=1+![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示的四枚邮票图片形状完全相同,分别是我国代科学家祖冲之、李时珍、张衡、僧一行.把四张图片混合在一起.

(1)若随机摸取一张图片,则摸到“祖冲之”图片的概率是__________;
(2)若随机摸取一张图片然后放回,再随机摸取一张图片,利用列表或树状图求两次至少有一次摸到“祖冲之”图片的概率;
(3)小东、小西、小南、小北四位同学依次摸取图片,若小东摸到“祖冲之”图片,则剩下三人中( )
A.小西摸到“李时珍”图片的概率大 B.小南摸到“李时珍”图片的概率大
C.小北摸到“李时珍”图片的概率大 D.三人摸到“李时珍”图片的概率一样大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点B在x轴上,点A、点C在双曲线y=![]() (k>0,x>0)上.若直线BC的解析式为y=
(k>0,x>0)上.若直线BC的解析式为y=![]() x﹣2,则k的值为( )
x﹣2,则k的值为( )
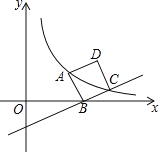
A.24B.12C.6D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2,照此规律作下去,则S1=_______,S2017=____________.
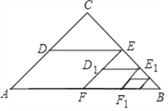
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化工厂要在规定时间内搬运1200吨化工原料.现有![]() ,
,![]() 两种机器人可供选择,已知
两种机器人可供选择,已知![]() 型机器人比
型机器人比![]() 型机器人每小时多搬运30吨型,
型机器人每小时多搬运30吨型,![]() 机器人搬运900吨所用的时间与
机器人搬运900吨所用的时间与![]() 型机器人搬运600吨所用的时间相等.
型机器人搬运600吨所用的时间相等.
(1)求两种机器人每小时分别搬运多少吨化工原料.
(2)该工厂原计划同时使用这两种机器人搬运,工作一段时间后,![]() 型机器人又有了新的搬运任务需离开,但必须保证这批化工原料在11小时内全部搬运完毕.问
型机器人又有了新的搬运任务需离开,但必须保证这批化工原料在11小时内全部搬运完毕.问![]() 型机器人至少工作几个小时,才能保证这批化工原料在规定的时间内完成?
型机器人至少工作几个小时,才能保证这批化工原料在规定的时间内完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D在AB的延长线上,C、E是⊙O上的两点,CE=CB,∠BCD=∠CAE,延长AE交BC的延长线于点F.
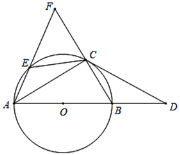
求证:(1)CD是⊙O的切线;
(2)CE=CF;
查看答案和解析>>
科目:初中数学 来源: 题型:
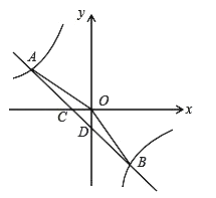
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第二、四象限内的
的图象交于第二、四象限内的![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() ,连接
,连接![]() ,且
,且![]() .
.
(1)求这个反比例函数和一次函数的解析式;
(2)根据图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com