
【题目】已知:在矩形ABCD中,AB=4,AD=10,点P是BC上的一点,若∠APD=90°,则AP=_____.
【答案】2![]() 或4
或4![]()
【解析】
设BP的长为x,则CP的长为(10-x),分别在Rt△ABP和Rt△DCP中利用勾股定理用x表示出AP2和DP2,然后在Rt△ADP中利用勾股定理得出关于x的一元二次方程,解出x的值,即可得出AP的长.
解:如图所示:
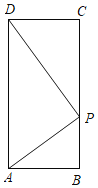
∵四边形ABCD是矩形,
∴∠B=∠C=90°,BC=AD=10,DC=AB=4,
设BP的长为x,则CP的长为(10-x),
在Rt△ABP中,由勾股定理得:
AP2=AB2+BP2=42+x2,
在Rt△DCP中,由勾股定理得:
DP2=DC2+CP2=42+(10-x)2,
又∵∠APD=90°,
在Rt△APD中,AD2=AP2+DP2,
∴42+x2+42+(10-x)2=102,
整理得:x2-10x+16=0,
解得:x1=2,x2=8,
当BP=2时,AP=![]() =
=![]() ;
;
当BP=8时,AP=![]() =
=![]() .
.
故答案为:![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知线段MN=3cm,在线段MN上取一点P,使PM=PN;延长线段MN到点A,使AN=![]() MN;延长线段NM到点B,使BN=3BM.
MN;延长线段NM到点B,使BN=3BM.
(1)根据题意,画出图形;
(2)求线段AB的长;
(3)试说明点P是哪些线段的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD= ![]() ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的对应点如图所示.
![]()
(1)在横线上填上“>”或“=”或“<”:
a 0,a-b 0,![]() .
.
(2)在数轴上标出表示有理数-a,-b,-c的点;
(3)用“>”把a,b,c,-a,-b,-c连接起来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.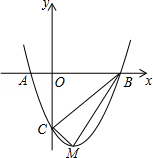
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以点P,A,C为顶点的三角形与△BCM相似?若存在,请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
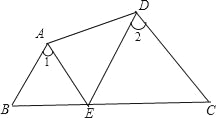
【题目】如图AB∥DE,∠1=∠2,试说明AE∥DC.下面是解答过程,请你填空或填写理由.
解:∵AB∥DE(已知)∴∠1= ( )
又∵∠1=∠2 (已知)∴∠2= (等量代换)
∴AE∥DC.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y= ![]() (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= ![]() (k≠0)上的点D1处,则a= .
(k≠0)上的点D1处,则a= . 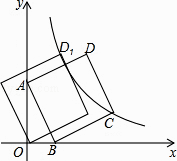
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com