
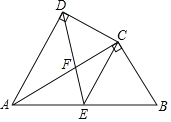
【题目】如图,四边形ABCD中,AC平分∠BAD,∠ADC=∠ACB=90°,E为AB的中点,AC与DE交于点F.
(1)求证:CE∥AD;
(2)求证:AC2=ABAD;
(3)若AC=2![]() ,AB=4,求
,AB=4,求![]() 的值.
的值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)欲证明CE∥AD,只要证明∠ACE=∠CAD即可;
(2)由AC平分∠DAB得∠DAC=∠CAB,加上∠ADC=∠ACB=90°,可证△ADC∽△ACB,根据相似三角形的性质即可得到结论;
(3)先求AD的长,CE的长,通过证明△AFD∽△CFE,可得![]() .
.
证明:(1)∵E为AB中点,∠ACB=90°
∴CE=![]() AB=AE,
AB=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
(2)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴![]() ,
,
∴AC2=ABAD;
(3)由(2)证得,AC2=ABAD,
∵AC=2![]() ,AB=4,
,AB=4,
∴12=4AD,
∴AD=3,
∵∠ACB=90°,E为AB的中点,
∴CE=![]() AB=2,
AB=2,
∵CE∥AD
∴△AFD∽△CFE,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相较于A(2,3),B(﹣3,n)两点.
的图象相较于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.

(1)根据图填写下表;
平均分 (分) | 中位数 (分) | 众数(分) | 极差 | 方差 | |
九(1)班 | 85 | ______ | 85 | ______ | 70 |
九(2)班 | 85 | 80 | ______ | ______ | ______ |
(2)结合两班复赛成绩的平均数和中位数、极差、方差,分析哪个班级的复赛成绩较好?
(3)如果在每班参加复赛的选手中分别选出2人参加决赛,你认为哪个班的实力更强一些,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=![]() x2+
x2+![]() x﹣4
x﹣4![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,作直线AC.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,作直线AC.
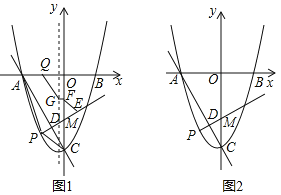
(1)如图1,点P是直线AC下方抛物线上的一点,连结PA,PC.过点P作PD⊥AC于点D,交y轴于点M,E是射线PD上的一点,Q是x轴上的一点,F是y轴上的一点,过F作该抛物线对称轴的垂线段,垂足为点G,连结EF,GQ.当△PAC面积最大时,求点P的坐标,并求EF+GQ+![]() (FG+QA)的最小值;
(FG+QA)的最小值;
(2)如图2,在(1)的条件下,将△CDM绕点D旋转得到△C'DM',在旋转过程中,当点C'或点M′落在y轴上(不与点M、C重合)时,将△C'DM'沿射线PD平移得到△C″D'M″,在平移过程中,平面内是否存在点N,使得四边形OM″NC″是菱形?若存在,请直接写出所有符合条件的点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
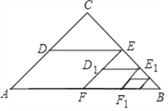
【题目】如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2,照此规律作下去,则S1=_______,S2017=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象相交于A,B两点,点A的坐标为(﹣1,3),点B的坐标为(3,n).
的图象相交于A,B两点,点A的坐标为(﹣1,3),点B的坐标为(3,n).
(1)求这两个函数的表达式;
(2)点P在线段AB上,且S△APO:S△BOP=1:3,求点P的坐标.
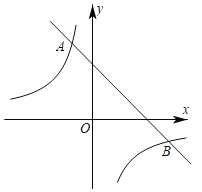
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化工厂要在规定时间内搬运1200吨化工原料.现有![]() ,
,![]() 两种机器人可供选择,已知
两种机器人可供选择,已知![]() 型机器人比
型机器人比![]() 型机器人每小时多搬运30吨型,
型机器人每小时多搬运30吨型,![]() 机器人搬运900吨所用的时间与
机器人搬运900吨所用的时间与![]() 型机器人搬运600吨所用的时间相等.
型机器人搬运600吨所用的时间相等.
(1)求两种机器人每小时分别搬运多少吨化工原料.
(2)该工厂原计划同时使用这两种机器人搬运,工作一段时间后,![]() 型机器人又有了新的搬运任务需离开,但必须保证这批化工原料在11小时内全部搬运完毕.问
型机器人又有了新的搬运任务需离开,但必须保证这批化工原料在11小时内全部搬运完毕.问![]() 型机器人至少工作几个小时,才能保证这批化工原料在规定的时间内完成?
型机器人至少工作几个小时,才能保证这批化工原料在规定的时间内完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
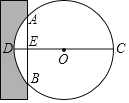
【题目】《九章算术》是我国古代著名数学著作,书中记载:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥DC于E,ED=1寸,AB=10寸,求直径CD的长.”则CD=_______寸.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学了一元二次方程的根与系数的关系后,小亮兴奋地说:“若设一元二次方程![]() 的两个根为
的两个根为![]() ,由根与系数的关系有
,由根与系数的关系有![]() ,
,![]() ,由此就能快速求出
,由此就能快速求出![]() ,
,![]() ,···的值了. 比如设
,···的值了. 比如设![]() 是方程
是方程![]() 的两个根,则
的两个根,则![]() ,
,![]() ,得
,得![]() .
.
![]() 小亮的说法对吗?简要说明理由;
小亮的说法对吗?简要说明理由;
![]() 写一个你最喜欢的元二次方程,并求出两根的平方和;
写一个你最喜欢的元二次方程,并求出两根的平方和;
![]() 已知
已知![]() 是关于
是关于![]() 的方程
的方程![]() 的一个根,求方程的另一个根与
的一个根,求方程的另一个根与![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com