
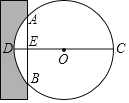
【题目】《九章算术》是我国古代著名数学著作,书中记载:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥DC于E,ED=1寸,AB=10寸,求直径CD的长.”则CD=_______寸.
 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
科目:初中数学 来源: 题型:
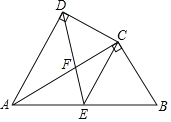
【题目】如图,四边形ABCD中,AC平分∠BAD,∠ADC=∠ACB=90°,E为AB的中点,AC与DE交于点F.
(1)求证:CE∥AD;
(2)求证:AC2=ABAD;
(3)若AC=2![]() ,AB=4,求
,AB=4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间为_________________
|
查看答案和解析>>
科目:初中数学 来源: 题型:
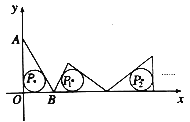
【题目】如图,在![]() 置于平面直角坐标系中,点
置于平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 内切圆的圆心.将
内切圆的圆心.将![]() 沿
沿![]() 轴的正方向作无滑动滚动,使它的三边依次与
轴的正方向作无滑动滚动,使它的三边依次与![]() 轴重合,第一次滚动后圆心为
轴重合,第一次滚动后圆心为![]() ,第二次滚动后圆心为
,第二次滚动后圆心为![]() ,…,依此规律,第2020次滚动后,
,…,依此规律,第2020次滚动后,![]() 内切圆的圆心
内切圆的圆心![]() 的坐标是__________.
的坐标是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点都在格点上.

(1)请按下列要求画图:
①将△ABC先向右平移5个单位,再向上平移1个单位,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2;
(2)若(1)所得的△A1B1C1与△A2B2C2,关于点P成中心对称,直接写出对称中心P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 为
为![]() 上动点(不与
上动点(不与![]() 、
、![]() 重合),作
重合),作![]() ,垂足为
,垂足为![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() 、
、![]() ,连接
,连接![]() 、
、![]() .
.
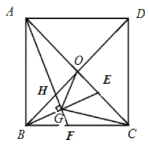
(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=-x2+bx+c的图象经过A(-2,-1),B(0,7)两点.
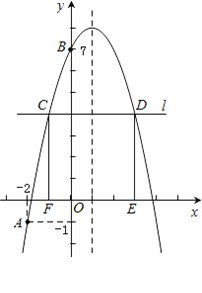
(1)求该抛物线的解析式及对称轴;
(2)当x为何值时,y>0?
(3)在x轴上方作平行于x轴的直线l,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作x轴的垂线,垂足分别为F,E.当矩形CDEF为正方形时,求C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x+2与反比例函数y2=![]() 的图象交于A,B两点,点A的坐标为(1,a).
的图象交于A,B两点,点A的坐标为(1,a).
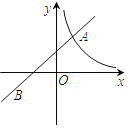
(1)求出k的值及点B的坐标;
(2)根据图象,写出y1>y2时x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com