
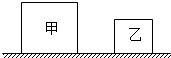
 如图所示,甲、乙两个不同材料制成的实心均匀正方体都放在水平地面上,它们的质量之比是16:9,边长之比为3:2.若在两个正方体的上部,沿水平方向分别截去相同高度的部分,则剩余部分的质量关系是m甲________m乙(填:“<”、“>”或“=”)
如图所示,甲、乙两个不同材料制成的实心均匀正方体都放在水平地面上,它们的质量之比是16:9,边长之比为3:2.若在两个正方体的上部,沿水平方向分别截去相同高度的部分,则剩余部分的质量关系是m甲________m乙(填:“<”、“>”或“=”)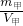 =
=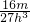 ,ρ乙=
,ρ乙=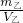 =
=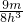 ,
,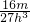 ×(3h)2×(3h-a)=
×(3h)2×(3h-a)=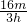 ×(3h-a),
×(3h-a),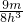 ×(2h)2×(2h-a)=
×(2h)2×(2h-a)=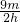 ×(2h-a),
×(2h-a),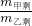 =
=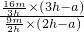 =
=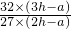 ,
,

 阅读快车系列答案
阅读快车系列答案科目:初中物理 来源: 题型:
 (2013?亳州模拟)如图所示,甲、乙两个均匀实心正方体分别放置在水平地面上,且它们各自对地面的压强相等.若分别在两个正方体的上部,沿水平方向截去相同高度后,则甲、乙的剩余部分对地面的压强P以及剩余部分质量m的大小关系为( )
(2013?亳州模拟)如图所示,甲、乙两个均匀实心正方体分别放置在水平地面上,且它们各自对地面的压强相等.若分别在两个正方体的上部,沿水平方向截去相同高度后,则甲、乙的剩余部分对地面的压强P以及剩余部分质量m的大小关系为( )查看答案和解析>>
科目:初中物理 来源: 题型:
 (2013?广安)用四只完全相同的滑轮和两根相同的绳子组成如图所示的甲、乙两个滑轮组,分别将两个相同的钩码提升10cm,若不计绳子与滑轮的摩擦,
(2013?广安)用四只完全相同的滑轮和两根相同的绳子组成如图所示的甲、乙两个滑轮组,分别将两个相同的钩码提升10cm,若不计绳子与滑轮的摩擦,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com