
 随着沉船“南澳一号”的发掘,海上丝绸之路逐渐引起了越来越多人的重视,这一条从汉朝就开始连通中国和世界的海上之路,在沉寂了几百年之后,再一次出现在世人面前.下图是水上打捞船起吊装置结构示意简图.某次打捞作业中,潜水员潜入水下9米深度将沉没于水下深处的货物固定,利用起吊装置打捞出水面,假设该货箱密封且体积为5m3,质量是20t.
随着沉船“南澳一号”的发掘,海上丝绸之路逐渐引起了越来越多人的重视,这一条从汉朝就开始连通中国和世界的海上之路,在沉寂了几百年之后,再一次出现在世人面前.下图是水上打捞船起吊装置结构示意简图.某次打捞作业中,潜水员潜入水下9米深度将沉没于水下深处的货物固定,利用起吊装置打捞出水面,假设该货箱密封且体积为5m3,质量是20t. =
=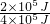 =50%
=50% 就能计算机械效率;
就能计算机械效率;

 名校课堂系列答案
名校课堂系列答案科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
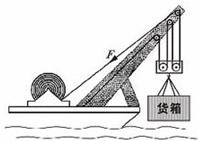 随着沉船“南澳一号”的发掘,海上丝绸之路逐渐引起了越来越多人的重视,这一条从汉朝就开始连通中国和世界的海上之路,在沉寂了几百年之后,再一次出现在世人面前.下图是水上打捞船起吊装置结构示意简图.某次打捞作业中,潜水员潜入水下9米深度将沉没于水下深处的货物固定,利用起吊装置打捞出水面,假设该货箱密封且体积为5m3,质量是20t.
随着沉船“南澳一号”的发掘,海上丝绸之路逐渐引起了越来越多人的重视,这一条从汉朝就开始连通中国和世界的海上之路,在沉寂了几百年之后,再一次出现在世人面前.下图是水上打捞船起吊装置结构示意简图.某次打捞作业中,潜水员潜入水下9米深度将沉没于水下深处的货物固定,利用起吊装置打捞出水面,假设该货箱密封且体积为5m3,质量是20t.查看答案和解析>>
科目:初中物理 来源:2010年湖北省黄冈市浠水县中考物理调研试卷(六)(解析版) 题型:解答题
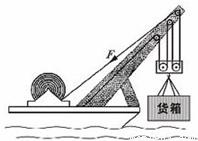
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com