
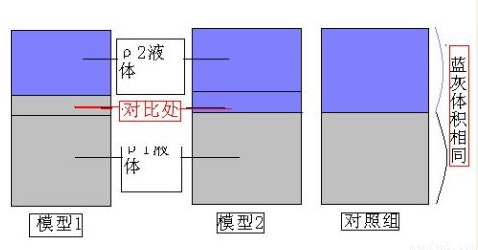
 解:模型1即为甲杯:由于ρ1<ρ2,两种液体的质量且各占一半.可得密度ρ1的液体体积大于密度ρ2的液体,密度ρ1的液体体积用灰标记,密度ρ2的液体体积用蓝色标记.
解:模型1即为甲杯:由于ρ1<ρ2,两种液体的质量且各占一半.可得密度ρ1的液体体积大于密度ρ2的液体,密度ρ1的液体体积用灰标记,密度ρ2的液体体积用蓝色标记.

科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源:不详 题型:单选题
| A.液体对甲杯底的压力大 |
| B.液体对乙杯底的压力大 |
| C.液体对甲、乙杯底的压力相等 |
| D.因为ρ1、ρ2不知谁在上,谁在下,所以无法判断压力大小 |
查看答案和解析>>
科目:初中物理 来源:2009年安徽省芜湖一中高一自主招生考试物理试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com