
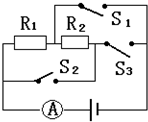
 如图所示,电源电压恒定,R1和R2阻值不随温度变化,当S1闭合后,S2、S3断开时,电流表示数为3A;当闭合S1、S2,断开S3时,电流表的示数为5A.当闭合S3断开S1、S2时,电路的总电阻与R1的比值是多少?电路消耗的总功率与R1上消耗的功率之比是多少?
如图所示,电源电压恒定,R1和R2阻值不随温度变化,当S1闭合后,S2、S3断开时,电流表示数为3A;当闭合S1、S2,断开S3时,电流表的示数为5A.当闭合S3断开S1、S2时,电路的总电阻与R1的比值是多少?电路消耗的总功率与R1上消耗的功率之比是多少?
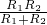 -------②
-------② R2.
R2. =
= =
= ;
; =
= =
= .
.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中物理 来源: 题型:
 从2011年5月1日起,执行酒驾重罚新规定.交警使用的某型号酒精测试仪的工作原理相当如图所示,电源电压恒为9V,传感器电阻R2的电阻值随酒精气体浓度的增大而减小,当酒精气体的浓度为0时,R2的电阻为80Ω.使用前要通过调零旋钮(即滑动变阻器Rl的滑片)对测试仪进行凋零,此时电压表的示数为8V.求:
从2011年5月1日起,执行酒驾重罚新规定.交警使用的某型号酒精测试仪的工作原理相当如图所示,电源电压恒为9V,传感器电阻R2的电阻值随酒精气体浓度的增大而减小,当酒精气体的浓度为0时,R2的电阻为80Ω.使用前要通过调零旋钮(即滑动变阻器Rl的滑片)对测试仪进行凋零,此时电压表的示数为8V.求:查看答案和解析>>
科目:初中物理 来源: 题型:
 (2013?大港区二模)在科技小组活动中,小明设计了一个电子秤,他想用电压表的读数来反映物体质量的大小,所用元件如图所示,电源电压恒为U,定值电阻的阻值为R0,滑动变阻器的总电阻为R,总长度为L,滑动触头固定在安放托盘的轻弹簧上并能随轻弹簧一起自由滑动,对托盘每施加1N的压力,弹簧的长度就会缩短△L,当托盘中不放物体时,电压表的示数为零:当在托盘中放物体时,电压表的示数与被测物体的质量成正比.
(2013?大港区二模)在科技小组活动中,小明设计了一个电子秤,他想用电压表的读数来反映物体质量的大小,所用元件如图所示,电源电压恒为U,定值电阻的阻值为R0,滑动变阻器的总电阻为R,总长度为L,滑动触头固定在安放托盘的轻弹簧上并能随轻弹簧一起自由滑动,对托盘每施加1N的压力,弹簧的长度就会缩短△L,当托盘中不放物体时,电压表的示数为零:当在托盘中放物体时,电压表的示数与被测物体的质量成正比.查看答案和解析>>
科目:初中物理 来源: 题型:
 某同学在做“调节灯泡亮度”的电学实验时,电路如图所示,电源电压恒为4.5V,电压表量程“0~3V”,滑动变阻器规格“20Ω l A”,灯泡L标有“2.5V 1.25W”字样(忽略灯丝电阻变化),在不损坏电路元件的情况下,下列判断正确的是( )
某同学在做“调节灯泡亮度”的电学实验时,电路如图所示,电源电压恒为4.5V,电压表量程“0~3V”,滑动变阻器规格“20Ω l A”,灯泡L标有“2.5V 1.25W”字样(忽略灯丝电阻变化),在不损坏电路元件的情况下,下列判断正确的是( )查看答案和解析>>
科目:初中物理 来源: 题型:
 交警使用的某型号酒精测试仪的工作原理如图所示,电源电压恒为9V.图中R1为酒精气体传感器,它的实质是一个电阻值随酒精气体浓度增大而减小的可变电阻.当酒精气体的浓度为0时,R1的阻值70Ω,电压表的示数为2V.求:
交警使用的某型号酒精测试仪的工作原理如图所示,电源电压恒为9V.图中R1为酒精气体传感器,它的实质是一个电阻值随酒精气体浓度增大而减小的可变电阻.当酒精气体的浓度为0时,R1的阻值70Ω,电压表的示数为2V.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com