
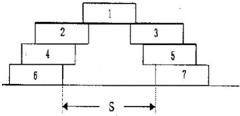
 如图所示,七块完全相同的砖块按照图示的方式叠放起来,每块砖的长度均为L,为保证砖块不倒下,6号砖块与7号砖块之间的距离S将不超过
如图所示,七块完全相同的砖块按照图示的方式叠放起来,每块砖的长度均为L,为保证砖块不倒下,6号砖块与7号砖块之间的距离S将不超过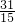 L
L L
L L
L ;当1放在2的边缘上时距离最大;
;当1放在2的边缘上时距离最大; -x)处;
-x)处; -x)=
-x)= x
x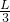 ;
; -x1)处;4受到的压力为G+
-x1)处;4受到的压力为G+ ;
; -x1)=(G+
-x1)=(G+ )x1;
)x1; 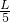 ;
;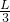 +
+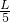 )=
)=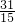 L;
L; 

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中物理 来源:2005年上海市第十九届初中物理竞赛初赛试卷(大同中学杯)(解析版) 题型:选择题

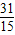 L
L L
L L
L查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com