
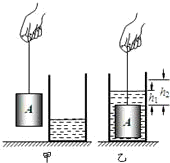
 如图甲所示,底面积为80cm2的圆筒形容器内装有适量的液体,放在水平桌面上;底面积为60cm2的圆柱形物体A悬挂在细绳的下端静止时,细绳对物体A的拉力为F1.将物体A浸没在圆筒形容器内的液体中,静止时,容器内的液面升高了7.5cm,如图乙所示,此时细绳对物体A的拉力为F2,物体A上表面到液面的距离为h1.然后,将物体A竖直向上移动h2,物体A静止时,细绳对物体A的拉力为F3.已知F1与F2之差为7.2N,F2与F3之比为5:8,h1为3cm,h2为5cm.不计绳重,g取10N/kg.则物体A的密度是________kg/m3.
如图甲所示,底面积为80cm2的圆筒形容器内装有适量的液体,放在水平桌面上;底面积为60cm2的圆柱形物体A悬挂在细绳的下端静止时,细绳对物体A的拉力为F1.将物体A浸没在圆筒形容器内的液体中,静止时,容器内的液面升高了7.5cm,如图乙所示,此时细绳对物体A的拉力为F2,物体A上表面到液面的距离为h1.然后,将物体A竖直向上移动h2,物体A静止时,细绳对物体A的拉力为F3.已知F1与F2之差为7.2N,F2与F3之比为5:8,h1为3cm,h2为5cm.不计绳重,g取10N/kg.则物体A的密度是________kg/m3.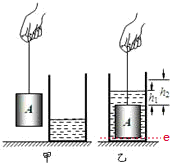 解:①v物=80cm2×7.5cm=600cm3,
解:①v物=80cm2×7.5cm=600cm3,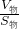 =
=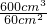 =10cm;
=10cm; ρ液=
ρ液= ×1.2×103kg/m3=2.8×103kg/m3;
×1.2×103kg/m3=2.8×103kg/m3;

科目:初中物理 来源: 题型:
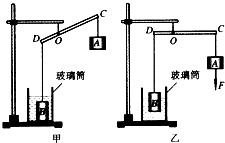 如图甲所示,底面积为50cm2的圆柱形玻璃筒中装有一定量的水,放在水平台面上,底面积为10cm2的圆柱形物体B浸没在水中,杠杆CD可绕支点O在竖直平面内转动,CO=2DO;物体A是质量100g的配重.如图乙所示,杠杆在水平位置平衡,作用在物体A上的方向向下的拉力F为0.6N,物体B有
如图甲所示,底面积为50cm2的圆柱形玻璃筒中装有一定量的水,放在水平台面上,底面积为10cm2的圆柱形物体B浸没在水中,杠杆CD可绕支点O在竖直平面内转动,CO=2DO;物体A是质量100g的配重.如图乙所示,杠杆在水平位置平衡,作用在物体A上的方向向下的拉力F为0.6N,物体B有| 2 |
| 5 |
| A、P的大小为500Pa |
| B、F浮的大小为0.2N |
| C、物体B的密度为7g/cm3 |
| D、物体B的体积为100cm3 |
查看答案和解析>>
科目:初中物理 来源: 题型:
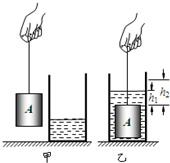 如图甲所示,底面积为80cm2的圆筒形容器内装有适量的液体,放在水平桌面上;底面积为60cm2的圆柱形物体A悬挂在细绳的下端静止时,细绳对物体A的拉力为F1.将物体A浸没在圆筒形容器内的液体中,静止时,容器内的液面升高了7.5cm,如图乙所示,此时细绳对物体A的拉力为F2,物体A上表面到液面的距离为h1.然后,将物体A竖直向上移动h2,物体A静止时,细绳对物体A的拉力为F3.已知F1与F2之差为7.2N,F2与F3之比为5:8,h1为3cm,h2为5cm.不计绳重,g取10N/kg.则物体A的密度是
如图甲所示,底面积为80cm2的圆筒形容器内装有适量的液体,放在水平桌面上;底面积为60cm2的圆柱形物体A悬挂在细绳的下端静止时,细绳对物体A的拉力为F1.将物体A浸没在圆筒形容器内的液体中,静止时,容器内的液面升高了7.5cm,如图乙所示,此时细绳对物体A的拉力为F2,物体A上表面到液面的距离为h1.然后,将物体A竖直向上移动h2,物体A静止时,细绳对物体A的拉力为F3.已知F1与F2之差为7.2N,F2与F3之比为5:8,h1为3cm,h2为5cm.不计绳重,g取10N/kg.则物体A的密度是查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
 如图甲所示,底面积为80cm2的圆筒形容器内装有适量的液体,放在水平桌面上;底面积为60cm2的圆柱形物体A悬挂在细绳的下端静止时,细绳对物体A的拉力为F1.将物体A浸没在圆筒形容器内的液体中,静止时,容器内的液面升高了7.5cm,如图乙所示,此时细绳对物体A的拉力为F2,物体A上表面到液面的距离为h1.然后,将物体A竖直向上移动h2,物体A静止时,细绳对物体A的拉力为F3.已知F1与F2之差为7.2N,F2与F3之比为 5:8,h1为3cm,h2为5cm.不计绳重,g取10N/kg.则液体的密度是
如图甲所示,底面积为80cm2的圆筒形容器内装有适量的液体,放在水平桌面上;底面积为60cm2的圆柱形物体A悬挂在细绳的下端静止时,细绳对物体A的拉力为F1.将物体A浸没在圆筒形容器内的液体中,静止时,容器内的液面升高了7.5cm,如图乙所示,此时细绳对物体A的拉力为F2,物体A上表面到液面的距离为h1.然后,将物体A竖直向上移动h2,物体A静止时,细绳对物体A的拉力为F3.已知F1与F2之差为7.2N,F2与F3之比为 5:8,h1为3cm,h2为5cm.不计绳重,g取10N/kg.则液体的密度是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com