精英家教网> 2025年全程助学与学习评估八年级数学上册浙教版 > 第1页 参考答案
2025年全程助学与学习评估八年级数学上册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册2025年全程助学与学习评估八年级数学上册浙教版答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 以下列长度的线段为边,不能构成三角形的是(
D
)
A.5,12,13
B.3,4,5
C.101,102,103
D.5,7,12
答案:D
解析:
根据三角形三边关系,任意两边之和大于第三边。
A. 5+12>13,5+13>12,12+13>5,能构成;
B. 3+4>5,3+5>4,4+5>3,能构成;
C. 101+102>103,101+103>102,102+103>101,能构成;
D. 5+7=12,不满足两边之和大于第三边,不能构成。
2. 在下列长度的四根木棒中,能与4cm,9cm长的两根木棒首尾相接构成一个三角形的是(
C
)
A.4cm
B.5cm
C.9cm
D.13cm
答案:C
解析:
设第三根木棒长度为x cm,根据三角形三边关系,两边之和大于第三边,两边之差小于第三边,可得9-4 < x < 9+4,即5 < x < 13。选项中只有9cm满足条件。
3. 如图,D是△ABC的边BC上的一点,则图中三角形个数为
3
个.
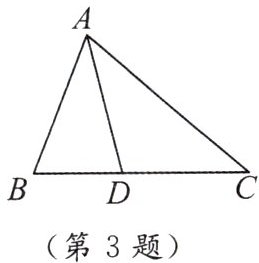
答案:3
解析:
以A为顶点,分别以BC上的线段为底边:线段BD、DC、BC,构成△ABD、△ADC、△ABC,共3个三角形。
4. 若△ABC中,∠A:∠B:∠C= 2:3:5,则∠A=
36°
,∠B=
54°
,∠C=
90°
.
答案:$\angle A = 36^{\circ}$,$\angle B = 54^{\circ}$,$\angle C = 90^{\circ}$(按题目要求填写对应角度值即可,这里以具体值呈现答案形式)即分别填$36^{\circ}$,$54^{\circ}$,$90^{\circ}$。
解析:
设$\angle A = 2x$,$\angle B = 3x$,$\angle C = 5x$。根据三角形内角和为$180^{\circ}$,有$2x + 3x + 5x = 180^{\circ}$,即$10x = 180^{\circ}$,解得$x = 18^{\circ}$。
所以$\angle A = 2×18^{\circ}=36^{\circ}$,$\angle B = 3×18^{\circ}=54^{\circ}$,$\angle C = 5×18^{\circ}=90^{\circ}$。
5. 按角分类,下列△ABC是什么三角形?说明理由.
(1)∠A= 60°,∠C= 80°.
(2)∠B= 40°,∠C= 50°.
(3)∠A= 30°,∠C= 45°.
答案:
(1)
∵∠A=60°,∠C=80°,
∴∠B=180°-∠A-∠C=180°-60°-80°=40°.
∵∠A、∠B、∠C均为锐角,
∴△ABC是锐角三角形.
(2)
∵∠B=40°,∠C=50°,
∴∠A=180°-∠B-∠C=180°-40°-50°=90°.
∵∠A=90°,
∴△ABC是直角三角形.
(3)
∵∠A=30°,∠C=45°,
∴∠B=180°-∠A-∠C=180°-30°-45°=105°.
∵∠B=105°>90°,
∴△ABC是钝角三角形.
6. 如图,已知D,E分别为△ABC中AC,AB边上任意两点(与点A不重合),比较AB+AC与BE+DE+CD的大小,并说明理由.
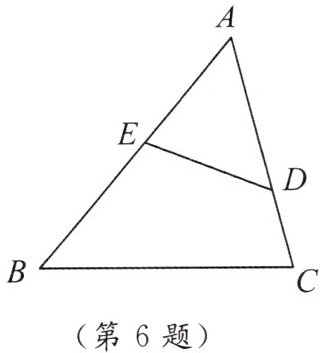
答案:AB+AC>BE+DE+CD.
理由如下:
∵E在AB上,
∴AB=AE+BE.
∵D在AC上,
∴AC=AD+CD.
∴AB+AC=AE+BE+AD+CD.
在△AED中,根据三角形两边之和大于第三边,得AE+AD>DE.
∴AE+AD+BE+CD>DE+BE+CD,即AB+AC>BE+DE+CD.


