精英家教网> 2025年全程助学与学习评估九年级数学上册浙教版 > 第1页 参考答案
2025年全程助学与学习评估九年级数学上册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册2025年全程助学与学习评估九年级数学上册浙教版答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列函数中,不一定是二次函数的是(
D
)
A.$ y = 5x^{2} + 1 $
B.$ y = - 2x^{2} + 3x $
C.$ y = - 5x^{2} $
D.$ y = ax^{2} + bx + c $
答案:D
解析:
形如$y = ax^{2}+bx + c$($a\neq0$,$a$、$b$、$c$是常数)的函数叫做二次函数。
选项A中$y = 5x^{2}+1$,其中$a = 5\neq0$,是二次函数;
选项B中$y=-2x^{2}+3x$,其中$a=-2\neq0$,是二次函数;
选项C中$y = - 5x^{2}$,其中$a=-5\neq0$,是二次函数;
选项D中$y = ax^{2}+bx + c$,当$a = 0$时,函数变为$y=bx + c$,是一次函数,不一定是二次函数。
2. 若二次函数 $ y = ( - 2x + 1 ) ^{2} - 5 $ 的二次项系数为 $ a $,一次项系数为 $ b $,常数项为 $ c $,则 $ b^{2} - 4ac = $
80
.
答案:80
解析:
将二次函数$y=(-2x + 1)^2 - 5$展开:$\begin{aligned}y&=( -2x)^2 + 2×(-2x)×1 + 1^2 - 5\\&=4x^2 - 4x + 1 - 5\\&=4x^2 - 4x - 4\end{aligned}$可得$a=4$,$b=-4$,$c=-4$。则$b^2 - 4ac=(-4)^2 - 4×4×(-4)=16 + 64=80$。
3. 某工厂第一年的利润为 30 万元,第三年的利润 $ y $(万元)与平均年增长率 $ x $ 之间的函数表达式是
$y = 30(1 + x)^{2}$
.
答案:$y = 30(1 + x)^{2}$
解析:
设平均年增长率为$x$,第一年的利润为30万元,则第二年的利润为$30(1 + x)$万元,第三年的利润相对于第二年继续增长$x$,则第三年的利润为$30(1 + x)(1 + x) = 30(1 + x)^{2}$万元。
所以,第三年的利润$y$(万元)与平均年增长率$x$之间的函数表达式是$y = 30(1 + x)^{2}$,且由于增长率$x$应为正数,所以$x$的取值范围为$x>0$(或写成$x$为实数且$x > - 1$且$x\neq0$等合理形式均可,题目未要求可不写出),该函数表达式已满足题目要求。
4. 正方形的边长为 3,若边长增加 $ x $,那么面积增加 $ y $,则 $ y $ 与 $ x $ 之间的函数表达式是(
C
)
A.$ y = x^{2} + 9 $
B.$ y = ( x + 3 ) ^{2} $
C.$ y = x^{2} + 6x $
D.$ y = 9 - x^{2} $
答案:C
解析:
原正方形边长为3,面积为 $3^2 = 9$。边长增加 $x$ 后,新边长为 $3 + x$,新面积为 $(3 + x)^2$。面积增加量为 $y = (3 + x)^2 - 9$,展开得 $y = 9 + 6x + x^2 - 9 = x^2 + 6x$。因此,$y$ 与 $x$ 的函数表达式为 $y = x^2 + 6x$。
5. 已知二次函数 $ y = 2x^{2} + bx - c $,当 $ x = - 2 $ 时,$ y = 0 $;当 $ x = 3 $ 时,$ y = 0 $.
(1)求 $ b $,$ c $ 的值.
(2)当 $ x = - 3 $ 时,求 $ y $ 的值.
答案:(1)将$x=-2$,$y=0$代入$y=2x^{2}+bx - c$,得$2×(-2)^{2}+b×(-2)-c=0$,即$8 - 2b - c=0$;将$x=3$,$y=0$代入,得$2×3^{2}+b×3 - c=0$,即$18 + 3b - c=0$。联立方程组$\begin{cases}8 - 2b - c=0\\18 + 3b - c=0\end{cases}$,两式相减得$10 + 5b=0$,解得$b=-2$,代入$8 - 2×(-2)-c=0$,得$c=12$。
(2)由(1)知二次函数为$y=2x^{2}-2x - 12$,当$x=-3$时,$y=2×(-3)^{2}-2×(-3)-12=18 + 6 - 12=12$。
(1)$b=-2$,$c=12$;(2)$12$
6. 如图,一块矩形草地的长为 100m,宽为 80m,欲在中间修筑两条互相垂直的宽为 $ x $(m)的小路,这时草坪的面积为 $ y $($ m^{2} $).求 $ y $ 与 $ x $ 的函数关系式,并求出 $ x $ 的取值范围.
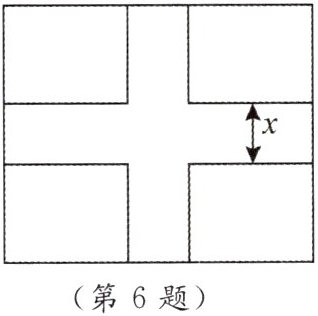
]
答案:由题意,两条小路互相垂直,宽均为$x$m。
矩形草地的长为$100$m,修筑一条宽为$x$m的纵向小路后,剩余草坪的长为$(100 - x)$m;宽为$80$m,修筑一条宽为$x$m的横向小路后,剩余草坪的宽为$(80 - x)$m。
草坪面积$y=(100 - x)(80 - x)$,展开得:
$y=100×80 - 100x - 80x + x² = x² - 180x + 8000$
因为小路宽$x$必须为正数,且不能超过草地的长和宽,所以$x > 0$,$100 - x > 0$,$80 - x > 0$,即$0 < x < 80$。
综上,$y$与$x$的函数关系式为$y = x² - 180x + 8000$,$x$的取值范围是$0 < x < 80$。

 ]
]