精英家教网> 2025年双休日作业延边教育出版社六年级数学上册人教版 > 第1页 参考答案
2025年双休日作业延边教育出版社六年级数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册2025年双休日作业延边教育出版社六年级数学上册人教版答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
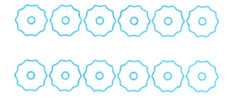
1. 看图写算式。

用加法计算:
$(
$\frac{1}{6}$
)+(
$\frac{1}{6}$
)+(
$\frac{1}{6}$
)=(
$\frac{1}{2}$
)$
用乘法计算:
$(
$\frac{1}{6}$
)×($
3
$)=(
$\frac{1}{2}$
)$
答案:$\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=\frac{1}{2}$;$\frac{1}{6}×3=\frac{1}{2}$
解析:
观察图形,每个圆被平均分成6份,涂色部分占1份,即每个圆表示的分数为$\frac{1}{6}$。
用加法计算:$\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=\frac{3}{6}=\frac{1}{2}$
用乘法计算:$\frac{1}{6}×3=\frac{3}{6}=\frac{1}{2}$
2.
新趋势 在标准大气压下,$1 \ g$氧气的体积约为$\frac {7}{10}L$,温度每升高$300 \ \celsius$,体积膨胀到原来的2倍,若温度升高$900 \ \celsius$,则$1 \ g$氧气的体积变约为(
5.6
)L。
答案:$\because$温度每升高$300 \ \celsius$,体积膨胀到原来的2倍,
$\therefore$若温度升高$900 \ \celsius$,体积膨胀到原来的$2^{900 ÷ 300} $倍,即$2^{3}$倍,
$\because$在标准大气压下,$1g$氧气的体积约为$\frac{7}{10}L$,
若温度升高$900 \ \celsius$,则$1g$氧气的体积变约为$\frac{7}{10} × 2^{3} = 5.6(L)$。
故答案为:$5.6$
3. 涂一涂,算一算。
(1)涂出$15$的$\frac{3}{5}$。

(2)涂出$12$的$\frac{5}{6}$。
答案:
(1)
解题步骤:$15×\frac{3}{5}$
$15$与$5$约分,$15÷5 = 3$,则$15×\frac{3}{5}=3×3 = 9$。
涂法:将$15$个小方格组成的图形平均分成$5$份,每份$3$个,涂其中$3$份,即涂$9$个小方格。
(2)
解题步骤:$12×\frac{5}{6}$
$12$与$6$约分,$12÷6 = 2$,则$12×\frac{5}{6}=2×5 = 10$。
涂法:将$12$个小方格组成的图形平均分成$6$份,每份$2$个,涂其中$5$份,即涂$10$个小方格。
4. 看图列式计算。
(1)
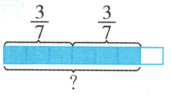
(
$\frac{3}{7}$
)×(
2
)=(
$\frac{6}{7}$
)
(2)一瓶饮料的容量是$\frac {9}{20}L$。

(
$\frac{9}{20}$
)×(
$\frac{1}{3}$
)=(
$\frac{3}{20}$
)(L)
答案:
(1)$\frac{3}{7} × 2 = \frac{6}{7}$
(2)$\frac{9}{20} × \frac{1}{3} = \frac{3}{20}$
5. 为大力加强劳动教育,老师带领五年级学生
在一块长方形基地里种植三种蔬菜(如下图),茄子的种植面积是多少平方米?

答案:1. 长方形基地面积:$24×8 = 192$(平方米)
2. 茄子占比:$1-\frac{1}{3}-\frac{3}{8}=\frac{24}{24}-\frac{8}{24}-\frac{9}{24}=\frac{7}{24}$
3. 茄子面积:$192×\frac{7}{24} = 56$(平方米)
答:茄子的种植面积是56平方米。
6.
易错题 两根同样长的铁丝,一根用去$\frac{2}{5} \ m$,另一根用去它的$\frac{2}{5}$,则用去的部分相比较,(
C
)。
A.第一根长
B.第二根长
C.无法比较
答案:C
解析:
设铁丝原长为$x$ m,第一根用去$\frac{2}{5} $m,用去长度固定;第二根用去$\frac{2}{5}x$ m,其长度随$x$变化。
若$x=1$,则第二根用去$\frac{2}{5} $m,两者相等;
若$x>1$,则$\frac{2}{5}x>\frac{2}{5}$,第二根用去部分更长;
若$x<1$,则$\frac{2}{5}x<\frac{2}{5}$,第一根用去部分更长。
由于铁丝长度未知,所以无法比较。
7. 如果大长方形的面积是$1$平方米,那么“求图中深色阴影部分的面积是多少平方米”的正确算式是(
A
)。
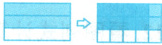
A.$\frac{2}{3} × \frac{1}{5}$
B.$\frac{2}{3} × \frac{4}{5}$
C.$\frac{1}{3} × \frac{1}{5}$
D.$\frac{2}{3} × \frac{8}{15}$
答案:A
解析:
大长方形面积为1平方米,先将其纵向平均分成3份,深色阴影占其中2份,即占大长方形的$\frac{2}{3}$;再将这$\frac{2}{3}$横向平均分成5份,深色阴影占其中1份,即占$\frac{2}{3}$的$\frac{1}{5}$。所以深色阴影面积算式为$\frac{2}{3}×\frac{1}{5}$。
8. 如果$a$是一个大于$0$的数,那么$a × \frac{2}{5}$和$a+ \frac{2}{5}$相比较,(
B
)。
A.$a × \frac{2}{5}$大
B.$a+ \frac{2}{5}$大
C.一样大
D.无法确定
答案:B
解析:
本题可通过作差法比较$a × \frac{2}{5}$与$a+ \frac{2}{5}$的大小,即计算$(a + \frac{2}{5})-a×\frac{2}{5}$,然后对其结果进行分析。
$(a + \frac{2}{5})-a×\frac{2}{5}=a + \frac{2}{5}-\frac{2}{5}a=\frac{3}{5}a+\frac{2}{5}$,
因为$a\gt0$,所以$\frac{3}{5}a\gt0$,则$\frac{3}{5}a+\frac{2}{5}\gt0$,即$(a + \frac{2}{5})-a×\frac{2}{5}\gt0$,所以$a + \frac{2}{5}\gt a×\frac{2}{5}$。
9. 看图写一写,算一算。

$\frac{($
2
$)}{($
3
$)} × \frac{($
1
$)}{($
3
$)} = \frac{($
2
$)}{($
9
$)}$
$\frac{($
3
$)}{($
4
$)} × \frac{($
4
$)}{($
5
$)} = \frac{($
3
$)}{($
5
$)}$
答案:$\frac{2}{3}×\frac{1}{3}=\frac{2}{9}$;$\frac{3}{4}×\frac{4}{5}=\frac{3}{5}$
解析:
左图:将长方形平均分成3列,取其中2列涂色表示$\frac{2}{3}$,再将这$\frac{2}{3}$平均分成3行,取其中1行深色涂色表示$\frac{1}{3}$,所以$\frac{2}{3}×\frac{1}{3}=\frac{2}{9}$;右图:将长方形平均分成4列,取其中3列涂色表示$\frac{3}{4}$,再将这$\frac{3}{4}$平均分成5行,取其中4行深色涂色表示$\frac{4}{5}$,所以$\frac{3}{4}×\frac{4}{5}=\frac{12}{20}=\frac{3}{5}$
10. 一条公路平均分给两个施工队修建。甲队
修完了自己任务的$\frac{2}{3}$,乙队修完了自己任务的$\frac{4}{7}$。甲队和乙队分别修完了这条公路的几分之几?
答案:设这条公路的整体长度为“1”。
每个施工队的任务为这条公路的$\frac{1}{2}$。
甲队修完了自己任务的$\frac{2}{3}$,
所以甲队修完了:
$\frac{1}{2} × \frac{2}{3} = \frac{1}{3}$。
乙队修完了自己任务的$\frac{4}{7}$,
所以乙队修完了:
$\frac{1}{2} × \frac{4}{7} = \frac{2}{7}$。
综上,甲队修完了这条公路的$\frac{1}{3}$;乙队修完了这条公路的$\frac{2}{7}$。








