
科目:高中数学 来源: 题型:
已知函数![]() 是在
是在![]() 上每一点均可导的函数,若
上每一点均可导的函数,若![]() 在
在![]() 时恒成立.
时恒成立.
(1)求证:函数![]() 在
在![]() 上是增函数;
上是增函数;
(2)求证:当![]() 时,有
时,有![]() ;
;
(3)请将(2)问推广到一般情况,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试(重庆卷)数学理工类模拟试卷(二) 题型:解答题
已知函数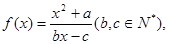 若方程
若方程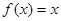 有且只有两个相异实根0,2,且
有且只有两个相异实根0,2,且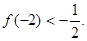
(Ⅰ)求函数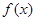 的解析式;
的解析式;
(Ⅱ)已知各项均不为1的数列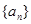 满足
满足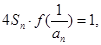 求通项
求通项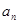 ;
;
(Ⅲ)如果数列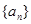 满足
满足 求证:当
求证:当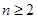 时恒有
时恒有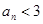 成立.
成立.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三上学期数学单元测试12-文科-算法、复数、推理与证明 题型:解答题
已知函数 是在
是在 上每一点均可导的函数,若
上每一点均可导的函数,若 在
在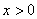 时恒成立.
时恒成立.
(1)求证:函数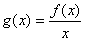 在
在 上是增函数;
上是增函数;
(2)求证:当 时,有
时,有 ;
;
(3)请将(2)问推广到一般情况,并证明你的结论(不要求证明).
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三上学期数学单元测试12-理科-算法、复数、推理与证明 题型:解答题
已知函数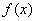 是在
是在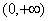 上每一点均可导的函数,若
上每一点均可导的函数,若 在
在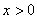 时恒成立.
时恒成立.
(1)求证:函数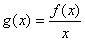 在
在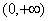 上是增函数;
上是增函数;
(2)求证:当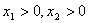 时,有
时,有 ;
;
(3)请将(2)问推广到一般情况,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com