Question

已知向量与，其中.

（1）问向量能平行吗？请说明理由；

（2）若，求和的值；

（3）在（2）的条件下，若，求的值.

 

Answer 1

（1）不能平行；（2），；（3）.

【解析】

试题分析：（1）先假设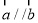，列方程得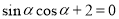，然后利用正弦的二倍角公式化简得，再判断此方程是否有解，若有解，可判断、可能平行；若无解，则可判断、不可能平行；（2）将向量的垂直问题转化为向量的数量积问题，得到，联立方程，并结合，即可求出；（3）先由同角三角函数的基本关系式计算出，然后再根据两角和的余弦公式展开计算得的值，最后结合的取值范围确定的值即可.

试题解析：【解析】
（1）向量不能平行

若平行，需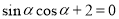，即，而

则向量不能平行 4分

（2）因为，所以 5分

即

又 6分

，即，

又 8分

（3）由（2）知

，得 9分

则 11分

又，则 12分.

考点：1.向量平行、垂直的判定与应用；2.同角三角函数的基本关系式；3.两角和与差的三角函数.