
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
分析 (Ⅰ)首先求出x,y的平均数,利用最小二乘法做出线性回归方程的系数,写出线性回归方程.
(Ⅱ)利用公式求出相关指数R2,即可得出结论.
解答 解:(Ⅰ) $\overline{x}=5$,$\overline{y}=50$;$\sum_{i=1}^5{{x_i}{y_j}}=1380$,$\sum_{i=1}^5{{x_i}^2}=145$;-----(2分)
则:$\hat b=\frac{{\sum_{i=1}^5{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^5{x_i^2-n{{\bar x}^2}}}}=\frac{1380-5×5×50}{{145-5×{5^2}}}=6.5$;$\hat a=\hat y-\hat b\overline{x}=50-6.5×5=17.5$
所以线性回归方程为:$\hat y=6.5x+17.5$--------------------------(4分)
(Ⅱ)$\sum_{i=1}^5{({y_i}}-{\hat y_i}{)^2}=155$,$\sum_{i=1}^5{({y_i}}-\bar y{)^2}=1000$;--------(1分)
${R^2}=1-\frac{{\sum_{i=1}^5{{{({y_i}-{{\hat y}_i})}^2}}}}{{\sum_{i=1}^5{{{({y_i}-\bar y)}^2}}}}$=$1-\frac{155}{1000}=0.845$.-----------------(3分)
即相关系数R2为0.845,证明残差变量对销售额的影响占15.5%.---(4分)
点评 本题考查回归分析的初步应用,考查求线性回归方程的求法,是一个综合题目,这种题目符合新课标的大纲要求,是一个典型的题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | $\frac{2015}{2}$ | C. | 2014 | D. | 1007 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | m | C. | 2m | D. | 4m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
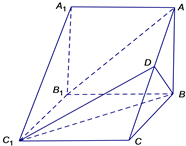 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AA1=AB=2,AB⊥BC,BC=3.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AA1=AB=2,AB⊥BC,BC=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com