
分析 (1)利用向量的数量积以及两角和与差的三角函数化简函数的表达式为一个角的一个三角函数的形式,利用余弦函数的单调增区间求出函数的单调增区间,即可求函数f(x)在[-π,π]上的单调递增区间;
(2)由题意:存在x∈[0,$\frac{π}{6}$],使f(x-$\frac{π}{4}$)>|m-2|,等价于f(x-$\frac{π}{4}$)max>|m-2|成立,只需要求f(x-$\frac{π}{4}$)max的值即可通过解不等式得到m的取值的范围.
解答 解:(1)向量$\overrightarrow{a}$=(2cosωx,1),$\overrightarrow{b}$=(2sin(ωx+$\frac{2π}{3}$),-$\sqrt{3}$),
∴f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=4cosωxsin(ωx+$\frac{2π}{3}$)-$\sqrt{3}$
化简得:f(x)=4cosωx(sinωxcos$\frac{2π}{3}$+cosωxsin$\frac{2π}{3}$)-$\sqrt{3}$
=-2sinωxcosωx+2$\sqrt{3}$cos2ωx-$\sqrt{3}$=-sin2ωx+$\sqrt{3}$+$\sqrt{3}$cos2ωx-$\sqrt{3}$=2cos(2ωx+$\frac{π}{6}$).
∵最小正周期为π,即T=π=$\frac{2π}{2ω}$,解得ω=1
∴f(x)=2cos(2x+$\frac{π}{6}$)
当x∈[-π,π]时,则:2x+$\frac{π}{6}$∈[-$\frac{11π}{6}$,$\frac{13π}{6}$]
由余弦函数图象可知:[-$\frac{7π}{12}$,-$\frac{π}{12}$]和[$\frac{5π}{12}$,$\frac{11π}{12}$]单调增区间.
(2)由题意:存在x∈[0,$\frac{π}{6}$],使f(x-$\frac{π}{4}$)>|m-2|成立,等价于f(x-$\frac{π}{4}$)max>|m-2|成立,
∵f(x)=2cos(2x+$\frac{π}{6}$)
∴f(x-$\frac{π}{4}$)=2cos(2x-$\frac{π}{3}$)
又∵x∈[0,$\frac{π}{6}$],∴2x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$]
那么:f(x-$\frac{π}{4}$)max=2
所以有:|m-2|<2,解得:0<m<4
故m的取值范围是(0,4).
点评 本题主要考查了三角函数的化简能力以及余弦函数性质的运用,值域的求法来解决恒成立的问题.属于中档题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:解答题
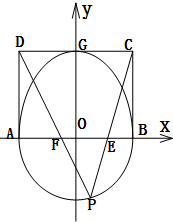 已知曲线C的图形如图所示,其上半部分是半椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1(y≥0)$,下半部分是半圆x2+y2=b2(y≤0),(a>b>0),半椭圆内切于矩形ABCD,且CD交y轴于点G,点P是半圆上异于A,B的任意一点,当点P位于点$M(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{3}}}{3})$时,△AGP的面积最大.
已知曲线C的图形如图所示,其上半部分是半椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1(y≥0)$,下半部分是半圆x2+y2=b2(y≤0),(a>b>0),半椭圆内切于矩形ABCD,且CD交y轴于点G,点P是半圆上异于A,B的任意一点,当点P位于点$M(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{3}}}{3})$时,△AGP的面积最大.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 64 | C. | 512 | D. | 1024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com