解:(I)(1)当过点P(1,2)的直线l与x轴垂直时,
此时圆心O到直线l的距离等于1,
所以x=1为所求直线方程.
(2)当过点P(1,2)且与x轴不垂直时,可设所求直线方程为y-2=k(x-1),
即:kx-y-k+2=0,由题意有
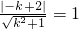
,解得

,
故所求的直线方程为

,即3x-4y+5=0.
综上,所求直线方程为x=1或3x-4y+5=0.
(II):设点P(x,y),M(x
0,y
0),则

=(x,y),
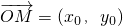
因为N(4,0)
所以

=(4,0)
因为

,
所以(x,y)=

[(4,0)+(x
0,y
0)]
即

,即

又x
02+y
02=4,∴(2x-4)
2+4y
2=4,
即:(x-2)
2+y
2=1.
故动点P的轨迹方程:(x-2)
2+y
2=1.
分析:(I)考虑两种情况:(1)斜率不存在即所求直线与y轴平行时,容易直线的方程;(2)斜率存在时,设出直线的斜截式,然后利用点到直线的距离公式列出原点到直线l的距离的方程,求出斜率k即可得到方程.
(II)设点P(x,y),根据点P和N的坐标,进而可得

和

,

,再代入

,答案可得.
点评:本题主要考查了点到直线的距离公式、利用向量的关系求点的轨迹方程.此题为中档题,学生做题时容易少一种斜率不存在的情况,要求学生考虑问题要全面.应用分类讨论的数学思想解决数学问题.

 ,求动点P的轨迹方程.
,求动点P的轨迹方程.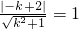 ,解得
,解得 ,
, ,即3x-4y+5=0.
,即3x-4y+5=0. =(x,y),
=(x,y),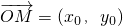
 =(4,0)
=(4,0) ,
, [(4,0)+(x0,y0)]
[(4,0)+(x0,y0)] ,即
,即
 和
和 ,
, ,再代入
,再代入 ,答案可得.
,答案可得.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 (1)如图,设圆O:x2+y2=a2的两条互相垂直的直径为AB、CD,E在弧BD上,AE交CD于K,CE交AB于L,求证:(
(1)如图,设圆O:x2+y2=a2的两条互相垂直的直径为AB、CD,E在弧BD上,AE交CD于K,CE交AB于L,求证:(