
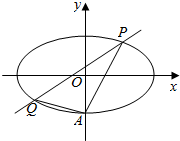
 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点A(0,-1),且离心率为$\frac{\sqrt{2}}{2}$.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点A(0,-1),且离心率为$\frac{\sqrt{2}}{2}$.分析 (Ⅰ)由题意可得b=1,结合椭圆的离心率及隐含条件求得a,则椭圆E的方程可求;
(Ⅱ)设出直线PQ的方程,联立直线方程和椭圆方程,然后借助于根与系数的关系整体运算得答案.
解答 解:(Ⅰ)由题意知$\frac{c}{a}=\frac{\sqrt{2}}{2}$,b=1,结合a2=b2+c2,解得$a=\sqrt{2}$,
∴椭圆的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(Ⅱ)由题设知,直线PQ的方程为y=k(x-1)+1 (k≠2),代入$\frac{{x}^{2}}{2}+{y}^{2}=1$,得
(1+2k2)x2-4k(k-1)x+2k(k-2)=0,
由已知△>0,设P(x1,y1),Q(x2,y2),x1x2≠0,
则${x}_{1}+{x}_{2}=\frac{4k(k-1)}{1+2{k}^{2}}$,${x}_{1}{x}_{2}=\frac{2k(k-2)}{1+2{k}^{2}}$,
从而直线AP与AQ的斜率之和:
${k}_{AP}+{k}_{AQ}=\frac{{y}_{1}+1}{{x}_{1}}+\frac{{y}_{2}+1}{{x}_{2}}=\frac{k{x}_{1}+2-k}{{x}_{1}}$$+\frac{k{x}_{2}+2-k}{{x}_{2}}$
=$2k+(2-k)(\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}})=2k+(2-k)\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$
=$2k+(2-k)\frac{4k(k-1)}{2k(k-2)}=2k-2(k-1)=2$.
点评 本题考查椭圆方程的求法,考查了椭圆的简单性质,涉及直线和圆锥曲线位置关系的问题,常采用联立直线方程和圆锥曲线方程,利用根与系数的关系求解,是中档题.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | Sn单调递减 | B. | Sn单调递增 | C. | Sn有最大值 | D. | Sn有最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{81}{4}$π | B. | 16π | C. | 9π | D. | $\frac{27}{4}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com