已知数列{an}满足a1=1,a2=λ(λ<3且λ≠-2),且an+2=an+1+6an.(n∈N*).
(1)证明:数列{an+1+2an}与数列{an+1-3an}都是等比数列;
(2)若an+1>an(n∈N*)恒成立,求λ的取值范围.
解析:(1)由a
n+2=a
n+1+6a
n得a
n+2+2a
n+1=3(a
n+1+2a
n)a
n+2-3a
n+1=-2(a
n+1-3a
n)…(4分)
由λ<3是λ≠-2知a
2+2a
1≠0,a
2-3a
1≠0,故有

∴数列{a
n+1+2a
n}与数列{a
n+1-3a
n}都是等比数列.…(6分)
(2)由(1)知:a
n+1+2a
n=(λ+2)3
n-1①a
n+1-3a
n=(λ-3)(-2)
n-1②…(7分)
由①-②得5a
n=(λ+2)3
n-1+(3-λ)(-2)
n-15a
n+1=(λ+2)3
n+(3-λ)(-2)
n…(8分)
∴5(a
n+1-a
n)=(2λ+4)•3
n-1+(3λ-9)•(-2)
n-1>0,又∵λ<3,
化简得
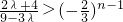
…(10分)
对于任意n∈N
*,总有
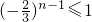
…(11分)
∴
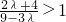
,解之得1<λ<3…(12分)
分析:(1)由等比数列的定义,将题设中的递推公式变形成(a
n+2+2a
n+1):(a
n+1+2a
n)=常数的形式即得;同理可证得数列{a
n+1-3a
n}都是等比数列;
(2)利用(1)中的结论,先求出a
n+1-a
n的表达式,化简得
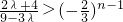
,再利用指数函数的性质建立关于λ的不等关系,即可解得λ的取值范围.
点评:本题考查了等比数列的定义,以及数列与不等式的综合,综合运用了分离参数法,难度一般.


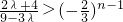 …(10分)
…(10分)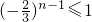 …(11分)
…(11分)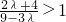 ,解之得1<λ<3…(12分)
,解之得1<λ<3…(12分)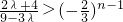 ,再利用指数函数的性质建立关于λ的不等关系,即可解得λ的取值范围.
,再利用指数函数的性质建立关于λ的不等关系,即可解得λ的取值范围.
