
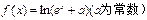 是定义在实数集R上的奇函数,函数
是定义在实数集R上的奇函数,函数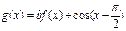 是区间
是区间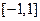 上的减函数。
上的减函数。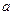 的值;
的值;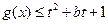 对
对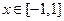 恒成立,求实数
恒成立,求实数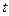 的取值范围;
的取值范围;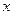 的方程
的方程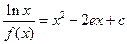 的实根的个数
的实根的个数科目:高中数学 来源:不详 题型:解答题
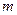 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为
米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为 万元。假设桥墩等距离分布,所有桥墩视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩视为点,且不考虑其他因素,记余下工程的费用为 万元。
万元。 关于
关于 的函数关系式;
的函数关系式;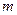 =640米时,需新建多少个桥墩才能使
=640米时,需新建多少个桥墩才能使 最小?
最小?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
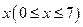 吨,应交水费为f(x),(1)求
吨,应交水费为f(x),(1)求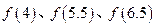 的值;(2)试求出函数f(x)的解析式。
的值;(2)试求出函数f(x)的解析式。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 是R上的减函数, 且
是R上的减函数, 且 的图象经过点
的图象经过点 (0, 4)和点
(0, 4)和点 (3, -2), 则当不等式 |f(x+t)-1|<3的解集为(-1, 2 ) 时,
(3, -2), 则当不等式 |f(x+t)-1|<3的解集为(-1, 2 ) 时,  的值为: ( )
的值为: ( ) 
| A.0 | B.-1 | C.1 | D.2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 0km/h的速度从
0km/h的速度从 甲地到达乙地,在乙地停留1小时后再以50km/h的速度返回甲地,把汽车离开甲地的距离s表示为时间t(从甲地出发时开始)的函数,求此函数表达式.
甲地到达乙地,在乙地停留1小时后再以50km/h的速度返回甲地,把汽车离开甲地的距离s表示为时间t(从甲地出发时开始)的函数,求此函数表达式.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 个分厂生产同一种电子产品,第一、二、三分厂的产量之比为
个分厂生产同一种电子产品,第一、二、三分厂的产量之比为 ,用分层抽样方法(每个分厂的产品为一层)从
,用分层抽样方法(每个分厂的产品为一层)从 个分厂生产的电子产品中共取
个分厂生产的电子产品中共取 件作使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为
件作使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为 ,
, ,
,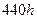 ,则抽取的
,则抽取的 件产品的使用寿命的平均值为 _ _h 。
件产品的使用寿命的平均值为 _ _h 。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com