
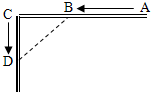
 汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)
汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)| 125(t2-16t+80) |
| 125[(t-8)2+16] |
| 125[(t-8)2+16] |
| 125×16 |
| 5 |
| 5 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2011年福建省罗源县第一中学高一上学期期中考试数学 题型:解答题
((本题13分)汽车和自行车分别从A地和C地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米。(汽车开到C地即停止)
(1)经过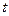 秒后,汽车到达B处,自行车到达D处,设B、D间距离为
秒后,汽车到达B处,自行车到达D处,设B、D间距离为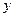 ,写出
,写出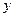 关于
关于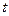 的函数关系式,并求出定义域。
的函数关系式,并求出定义域。
(2)经过多少时间后,汽车和自行车之间的距离最短?最短距离是多少?
查看答案和解析>>
科目:高中数学 来源:2011年福建省高一上学期期中考试数学 题型:解答题
((本题13分)汽车和自行车分别从A地和C地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米。(汽车开到C地即停止)
(1)经过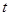 秒后,汽车到达B处,自行车到达D处,设B、D间距离为
秒后,汽车到达B处,自行车到达D处,设B、D间距离为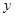 ,写出
,写出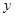 关于
关于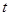 的函数关系式,并求出定义域。
的函数关系式,并求出定义域。
(2)经过多少时间后,汽车和自行车之间的距离最短?最短距离是多少?

查看答案和解析>>
科目:高中数学 来源:2011--2012学年山西省第一学期高一月考数学试卷 题型:解答题
汽车和自行车分别从A地和C地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米。(汽车开到C地即停止)
(1)经过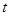 秒后,汽车到达B处,自行车到达D处,设B、D间距离为
秒后,汽车到达B处,自行车到达D处,设B、D间距离为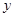 ,写出
,写出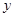 关于
关于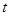 的函数关系式,并求出定义域。
的函数关系式,并求出定义域。
(2)经过多少时间后,汽车和自行车之间的距离最短?最短距离是多少?

查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省温州市龙湾中学高一(上)第一次月考数学试卷(解析版) 题型:解答题
 汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)
汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com