
 如图,P是圆x2+y2=4上的动点,P点在x轴上的投影是D,点M满足
如图,P是圆x2+y2=4上的动点,P点在x轴上的投影是D,点M满足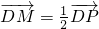 .
.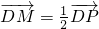 .
. ,其图形为椭圆.
,其图形为椭圆.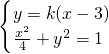 得(1+4k2)x2-24k2x+36k2-4=0
得(1+4k2)x2-24k2x+36k2-4=0 ,
,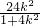 ,y1+y2=k(x1+x2-6)=
,y1+y2=k(x1+x2-6)=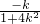 ;
; ,即
,即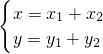 ,
,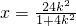 ,y=
,y=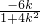 ,
, .
.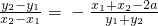 =-
=- ,
,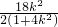 =
= ,0<k2<
,0<k2< ,解得0<a<1,
,解得0<a<1, ,即可求得顶点E的轨迹方程;(3)若存在点Q(a,0),使得四边形QAFB为菱形,可得QA=AB,代入,因式分解,利用韦达定理,用k表示a,转化为求函数的值域问题.
,即可求得顶点E的轨迹方程;(3)若存在点Q(a,0),使得四边形QAFB为菱形,可得QA=AB,代入,因式分解,利用韦达定理,用k表示a,转化为求函数的值域问题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
 已知抛物线x2=2py(p>0).抛物线上的点M(m,1)到焦点的距离为2
已知抛物线x2=2py(p>0).抛物线上的点M(m,1)到焦点的距离为23
| ||
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•浙江模拟)已知抛物线x2=4y.
(2012•浙江模拟)已知抛物线x2=4y.查看答案和解析>>
科目:高中数学 来源: 题型:
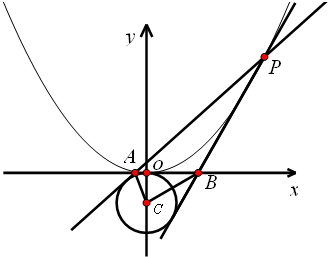
 (2011•武昌区模拟)如图,已知点P是圆C:x2+(y-2
(2011•武昌区模拟)如图,已知点P是圆C:x2+(y-2| 2 |
| OP |
| OQ |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省五校第二次联考数学试卷(文科)(解析版) 题型:解答题
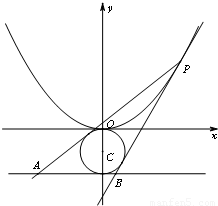
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com