分析:(1)本题适合建立空间坐标系得用向量法解决这个立体几何问题,建立空间坐标系,给出有关点的坐标,设出点F的坐标,求异面直线AE与A1F的方向向量,利用利用夹角公式求异面直线AE与A1F所成角的余弦值即可.
(2)分别同平面AEF的法向量为和平面A1EF的一个法向量.再根据平面AEF⊥平面A1EF,得出向量的数量积为0,即可求解得λ的值.
解答: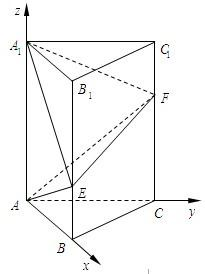
解:建立如图所示的空间直角坐标系A-xyz.
(1)设a=1,则AB=AC=1,AA
1=3,
各点的坐标为A(0,0,0),E(1,0,1),
A
1(0,0,3),F(0,1,2).
=(1,0,1),
=(0,1,-1).
∵
||=||=,
•=-1,
∴
cos?,?===-.
∴向量
和
所成的角为120
o,
∴异面直线AE与A
1F所成角为60°;(4分)
(2)∵
E(a,0,),
F(0,a,),
∴
=(a,0,),=(0,a,).
设平面AEF的法向量为n
1(x,y,z),
则
n1•=0,且
n1•=0.
即
ax+=0,且
ay+=0.
令z=1,则
x=-,y=-.
∴
n1=(-,-,1)=
(-,-,1)是平面AEF的一个法向量.(6分)
同理,
n2=(,,1)=
(,,1)是平面A
1EF的一个法向量.(8分)
∵平面AEF⊥平面A
1EF,∴n
1•n
2=0.∴
--+1=0.
解得,
λ=.
∴当平面AEF⊥平面A
1EF时,
λ=.
点评:考查用空间向量为工具解决立体几何问题,此类题关键是找清楚线的方向向量、面的法向量以及这些向量内积为0、共线等与立体几何中线面、面面位置关系的对应,考查空间想象能力和思维能力.

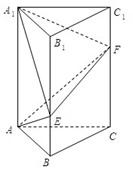 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90o,AB=AC=a,AA1=b,点E,F分别在棱BB1,CC1上,且BE=
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90o,AB=AC=a,AA1=b,点E,F分别在棱BB1,CC1上,且BE= 解:建立如图所示的空间直角坐标系A-xyz.
解:建立如图所示的空间直角坐标系A-xyz.





