
 ,bn=(n+1)2,n∈N+.
,bn=(n+1)2,n∈N+. ,n∈N+.
,n∈N+.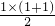 ,等式成立.
,等式成立.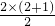 ,等式成立.
,等式成立. ,k≥2.
,k≥2.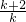 ak=
ak=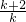 •
•
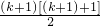 .
. 对任何的n∈N+都成立.
对任何的n∈N+都成立. ]2=(k+1)2•bk+1.
]2=(k+1)2•bk+1. ,bn=(n+1)2,n∈N+.先证an=
,bn=(n+1)2,n∈N+.先证an= ,n∈N+.再证bn=(n+1)2,n∈N+.
,n∈N+.再证bn=(n+1)2,n∈N+.

科目:高中数学 来源: 题型:
| A、某校高三1班有55人,2班有54人,3班有52人,由此得高三所有班人数超过50人 | ||||
| B、两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则∠A+∠B=180° | ||||
| C、由平面三角形的性质,推测空间四面体性质 | ||||
D、在数列{an}中a1=1,an=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则∠A+∠B=180° | ||||
| B、某校高二(1)班有55人,高二(2)班有52人,由此得高二所有班人数超过50人 | ||||
| C、由平面三角形的性质,推出空间四边形的性质 | ||||
D、在数列{an}中,a1=1,an=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com