
5名运动员争夺3项比赛冠军(每项比赛无并列冠军),获得冠军的可能种数为:
A.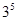 | B.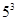 | C.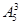 | D.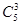 |
B
解析试题分析:题是一个分步计数问题,5名学生中任一名均可报其中的任一项,因此每个学生都有4种报名方法,第一个学生有4种报名方法,第二个也是这样,以此类推5名学生都报了项目才能算完成这一事件.根据分步乘法原理得到结果.每个项目只有一个冠军,每一名学生都可能获得其中的一项获军,因此每个项目获冠军的可能性有5种,根据分步乘法原理得到结果.解:由题意知,本题是一个分步计数问题, 5名学生中任一名均可报其中的任一项,因此每个学生都有4种报名方法,5名学生都报了项目才能算完成这一事件.故报名方法种数为3×3×3×3×3=35种.每个项目只有一个冠军,每一名学生都可能获得其中的一项获军,因此每个项目获冠军的可能性有5种.∴n=5×5×5=53种
考点:分步计数原理
点评:本题考查分步计数原理,是一个易错题,易错点是不能正确的理解分步原理,本题是一个典型的分步计数原理的应用.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:044
(1)5
名学生从3项体育项目中选择参赛,若每一名学生只能参加一项,则有多少种不同的参赛方法?(2)
若5名学生争夺3项比赛冠军(每一名学生参赛项目不限),则冠军获得者有几种不同情况(没有并列冠军)?查看答案和解析>>
科目:高中数学 来源: 题型:
(2)数、理、化三科教师都布置了作业,求在同一时刻5名学生都做作业的所有可能情况的种数.
查看答案和解析>>
科目:高中数学 来源:2014届海南琼海高二下学期教学质量监测理科数学试卷(解析版) 题型:选择题
5名运动员争夺3项比赛冠军(每项比赛无并列冠军),获得冠军的可能种数为:
A.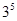 B.
B.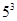 C.
C.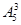 D.
D.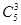
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com