
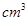 ,高为2
,高为2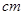 长方体的无盖铁盒,问这个铁盒底面的长和宽各为多少时材料最省?
长方体的无盖铁盒,问这个铁盒底面的长和宽各为多少时材料最省?  培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源:不详 题型:解答题
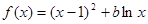 ,其中
,其中 为常数.
为常数.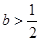 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;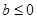 时,求
时,求 的极值点并判断是极大值还是极小值;
的极值点并判断是极大值还是极小值; ,不等式
,不等式 都成立.
都成立.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 万元满足
万元满足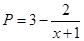 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为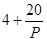 元.
元.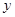 万元表示为促销费用
万元表示为促销费用 万元的函数;
万元的函数;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
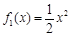 ,
,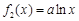 (其中
(其中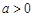 ).
).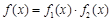 的极值;
的极值;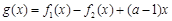 在区间
在区间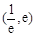 内有两个零点,求正实数a的取值范围;(Ⅲ)求证:当
内有两个零点,求正实数a的取值范围;(Ⅲ)求证:当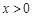 时,
时,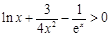 .(说明:e是自然对数的底数,e=2.71828…)
.(说明:e是自然对数的底数,e=2.71828…)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
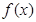 满足
满足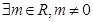 ,对定义域内的任意
,对定义域内的任意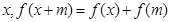 恒成立,则称
恒成立,则称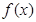 为m函数,现给出下列函数:
为m函数,现给出下列函数: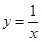 ; ②
; ②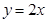 ; ③
; ③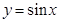 ; ④
; ④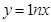
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com